【目标检测】一、初始的R-CNN与SVM

1.流程

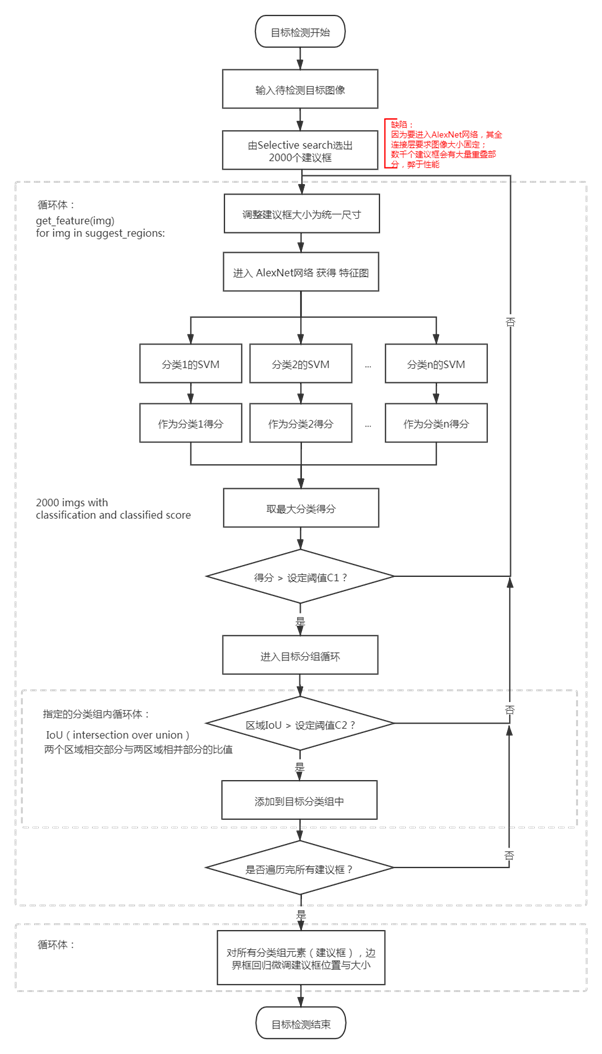
为什么要用SVM而不是CNN最后一层的softmax？

取什么模型必然是有标准衡量，这个流程取得是书上[4]写的，作者说他得实验证明SVM比FC的mAP要高，所以我流程暂且这样画了。

R-CNN取的是alexNet的迁移学习进行微调，它原来的训练数据就是随机的，而为了避免正样本数据过小导致卷积网络过拟合，正样本的框中没有SVM训练时严格，

也即说，训练中，相同的数据，在SVM里正样本卡得更严格，让SVM判别是正样本的概率也会低一些，那SVM的mAP高一些也能理解。

那么又有一个新问题，既然alexNet后接softmax结果不理想，那用fc+softmax替代svm呢？这个讨论在下节。

（刚好有一个图说明这个mAP怎么算，它更关注在确实有目标的建议框里面，模型给出的“信心”是多少）

引自：https://blog.csdn.net/asasasaababab/article/details/79994920

2.数学概念

SVM（Support Vector Machines），主要想找到分离一批数据的超平面，约定是，找到距离这个超平面最近的点做距离该点最远的线（/面）。

支持向量（support vecotr）就是离超平面最近的点，SVM由此命名。

而规划超平面涉及到核（Kernal）函数概念，最终计算SVM会是解决不等式约束问题，这里面就有多种方式。

（原始的SVM仅用于二分类，分类标签按计算需求确定，可能是0和1，或者是-1和1，以此区分两个类别。多种分类需要动刀函数距离）

对于一个二维平面来说，如果能用一条直线区分出两批数据，那么如何确定这条直线呢（可能会有多条），

SVM原则是找到两批数据中点距离目标线最近的点，距离最大的解。这听起来有很多个未知数

已知点A，假设超平面表达式（目标函数）为 ，那么点A对y的距离（推导过程让人脑闭，有需要再深究）：

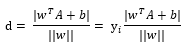
这个yi是取-1和1的标签值，注，yi的i不同书写在了不同位置（上标或下标），但都是表示标签。

为了下文计算方便，把分子拎出来，为了掉绝对值，此处添加变量yi（表示标签值，i = 1,2,3,..n，表示第几个数据）[2]，

yi取-1或1，以使分子结果不变，

设定下式为函数距离（或称为函数间隔），可以表示点到超平面的距离远近。

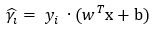
目标是找到函数距离最小值，

下一步是求距离超平面最近的点对超平面的距离最大化之解：

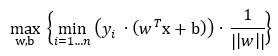
优化问题，分成两个整体来处理，

已知要求的函数间隔最小，那么有：

整理一下，

又  不影响margin取值，此处可令其为1，（？[2]笔者并不太明白），

求||w||最小值等价于||w||²/2的最小值，为了求导方便，上式可转化为：

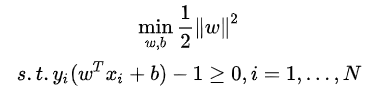
为了求解线性可分支持向量机的最优化问题，将它作为原始最优化问题，

应用拉格朗日对偶性，通过求解对偶问题(dual problem)得到原始问题(primal problem)的最优解，这就是线性可分支持向量机的对偶算法，

这样做的优点：一是对偶问题往往更容易求解；二是自然引入核函数，进而推广到非线性分类问题。

——《统计学习方法》

关于如何求解拉格朗日此处不叙述，详见[2][3]，

拉格朗日乘数法式子：

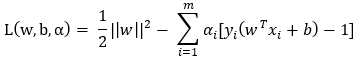
省略化简，得到约束：

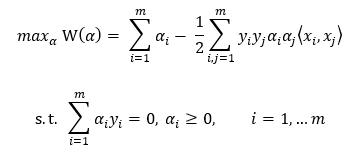
注，尖括号表示向量内积（也即点积）。

由于此时假设数据100%线性可分，然而真实数据并不都是那么“干净”，此处引入松弛变量（slack variable），以允许有些数据点处于分隔面错误的一侧，约束条件变为：C≥α ≥ 0 ，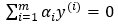

如何求解，传统地有二次规划求解（quadratic solver），但是这个计算量大，John Platt发布了一个叫SMO（Sequential Minimal Optimization，序列最小优化）的算法以减少计算。

简化的SMO伪代码：

创建一个α向量并将其初始化为0的向量

当迭代次数小于最小迭代次数时（外循环）：

对数据集中的每个数据向量（内循环）：

　　如果该数据向量可以被优化：

　　　　随机选择另外一个数据向量

　　　　同时优化这两个向量

　　　　如何这两个向量不能被同时优化，退出内循环

如果所有向量都没被优化，增加迭代数目，继续下一次循环

核（kernel）函数

如果一批数据并没有呈现明显的直线划分规律，例如呈现环分布的划分规律，

那么求解这个低纬度的非线性问题，最好就把它转化成高纬度的线性问题，前者转化到后者，这个映射过程用核函数满足。

因为SVM的向量都是内积表示，这里面把内积运算替换成核函数的方式，就叫做核技巧（kernel trick）或核变电（kernel substation）。

径向基核函数（Radial Basis Function），是某种沿径向对称的标量函数，是一个常用的度量两个向量距离的核函数。

例如，线性问题，是 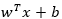，非线性问题，假设核函数取径向基函数的高斯版本：

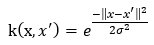
（？）其中，σ是用户定义的用于确定到达率（reach）或者说函数值跌落到0的速度参数。

def kernelTrans(X, A, kTup):
  m,n = shape(X)
  K = mat(zeros((m, 1)))
  if kTup[0] == 'lin' : K = X*A.T
  elif kTup[0] == 'rbf' :
      for j in range(m):
          deltaRow = X[j, :] – A  # 公式
          K[j] = deltaRow*deltaRow.T  # 平方
      K = exp(K / (-1*kTup[1]**2))  # 元素间的除法
  else : raise NameError('That Kernel is not recognizaed~ ')
  return K

class optStruct:
  def __init__(self, dataMatIn, classLabels, C, toler, kTup):
      self.X = dataMatIn
      …
      self.m = shape(dataMatIn)[0]
      self.K = mat(zeros((self.m, self.m)))
      for i in range(self.m):
          self.K[:,i] = kernalTrans(self.X, self.X[i, :], kTup)

SVM用于数值型数据，可视化分割超平面，其主要求解在于两个变量的调优，几乎所有分类问题都能用它，

原始的SVM是一个二分类器，应对多类问题需要调整SVM，

但其核函数的选择，以及核函数里自定义变量的影响，使得这个最优解需要大量训练。

=======================================================

资料：

[1] https://baike.baidu.com/item/拉格朗日乘数法/8550443?fromtitle=拉格朗日乘子法

[2] https://zhuanlan.zhihu.com/p/146515617

[3] https://blog.csdn.net/m0_37687753/article/details/80964472?spm=1001.2014.3001.5501

[4]杜鹏、谌(chen2)明、苏统华 编著《深度学习与目标检测》

Peter Harrington著《机器学习实战》

https://blog.csdn.net/m0_37687753/article/details/80964487

https://blog.csdn.net/laobai1015/article/details/82763033

https://baike.baidu.com/item/函数间隔/23224467?fr=aladdin

按这个计算原理来说，如果有一份数据，代入到SVM的分隔面里，为0是在面上，如果值>0，是正分类，<0是负分类；

此处可以观察到，如果值越大，即距离分隔面越远，那分类正确性也会越大。

如何改造SVM处理多种分类呢？

改造SVM为多分类识别：

1 直接法：在目标函数上修改，将多个分类面的参数求解合并成一个最优化问题，这种计算复杂，仅适合小型问题。

2 间接法：把多分类转变成多个二分类问题，常见有one-against-one和one-against-all两种。

一对多（one-versus-rest，简称OVR SVMs）

K个分类就有k个SVM，例如ABC..N共n个分类，那么

SVM1：设A为正集，BC..N为负集；

SVM2：设B为正集，AC..N为负集；

……

SVMn：设N为正集，AB..(N-1)为负集；

一对一（one-versus-one）

K个分类就有k(k-1)/2个SVM，排列组合任意两个分类做SMV，再总体计算单个分类得分。

层次SVM，把分类做成二叉树结构。

资料：

http://blog.itpub.net/29829936/viewspace-2168864/

3.应用代码

笔者还没有实现过，暂且搁置。