决策树算法之ID3与C4.5的理解与实现

github：代码实现
本文算法均使用python3实现

---

1. 决策树

  决策树（decision tree）是一种基本的分类与回归方法（本文主要是描述分类方法），是基于树结构进行决策的，可以将其认为是if-then规则的集合。一般的，一棵决策树包含一个根节点、若干内部节点和若干叶节点。其中根节点包含所有样本点，内部节点作为划分节点（属性测试），叶节点对应于决策结果。

  用决策树进行分类，是从根节点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子节点，若该子节点仍为划分节点，则继续进行判断与分配，直至将实例分到叶节点的类中。

  若对以上描述不太明白，可以结合以下图进行理解。

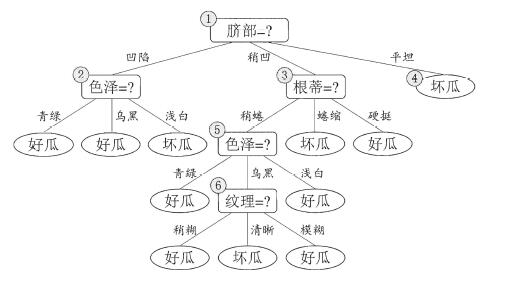
  根据以上决策树，现在给你一个实例：{色泽：青绿，根蒂：稍蜷，敲声：清脆，纹理：清晰，脐部：稍凹，触感：光滑}，来判断该瓜是否是好瓜。其过程是：脐部（稍凹）-->根蒂（稍蜷）-->色泽（青绿）-->好瓜。

  以上是由决策树来进行分类的过程。而决策树的学习（构建）通常是一个递归地选择最优特征的过程。那么构建决策树时如何选择特征作为划分点（即选择哪个特征作为根节点或者选择哪个特征作为非叶子节点）？当训练数据量大、特征数量较多时构建的决策树可能很庞大，这样的决策树用来分类是否好？

  由这些问题我们可以知道，构建决策树的三个要点：
  （1）特征选择
  （2）决策树的生成
  （3）决策树修剪

---

2. ID3算法

  基于ID3算法的决策树构建，其选择特征的准则是信息增益。信息增益（information gain）表示得知特征 $ X $ 的信息而使得类 $ Y $ 的信息的不确定性减少的程度。也就是说，信息增益越大，通过特征 $ X $ ，就越能够准确地将样本进行分类；信息增益越小，越无法准确进行分类。

  在介绍信息增益之前，我们需要先对熵进行一下讲解。

2.1 熵（Entropy）

  熵是度量样本集合纯度最常用的一种指标，它是信息的期望值。我们首先了解一下什么是信息。由《机器学习实战》中定义：

如果待分类的事务可能划分在多个分类之中，则符号（特征） $ k $ 的信息定义为： \[ l(k)=-\log_2{p(k)} \]
其中 $ p(k) $ 为选择该分类的概率。

  而熵计算的是所有类别所有可能值包含的信息期望值，其公式为：\[ Ent(D)=-\sum_{k=1}^N{p(k)\log_2{p(k)}} \]
  其中 $ N $ 为类别个数。

  现在我们使用例子，来理解熵的计算：

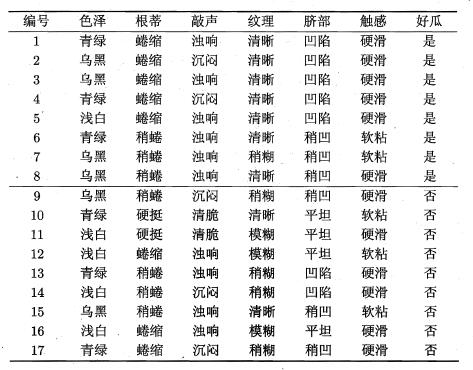
  （1）对于最终分类（是否为好瓜），计算其信息熵：
    由上表可看出，一共有17个样本，属于好瓜的有8个样本，坏瓜的有9个样本，因此其熵为：\[ Ent(D) = -\sum_{k=1}^2{p_k\log_2{p_k}}= - ( \frac{8}{17}\log_2\frac{8}{17} + \frac{9}{17}\log_2\frac{9}{17})=0.998 \]
  （2）对于特征“色泽”，计算其信息熵：
    由于特征“色泽”取值有：{青绿，乌黑，浅白}。若使用该属性对 $ D $ 进行划分，可得到3个子集，分别记为： $ D_1 $ （色泽=青绿）， $ D_2 $ （色泽=乌黑）， $ D_3 $ （色泽=浅白）。

    其中 $ D_1 $ 包含样本 $ {1,4,6,10,13,17} $ ,其中类别为好瓜的比例为 $ p_1=\frac{3}{6} $ ，坏瓜的比例为 $ p_2=\frac{3}{6} $ ； $ D_2 $ 包含样本 $ {2,3,7,8,9,15} $ ,其中类别为好瓜的比例 $ p_1=\frac{4}{6} $ ，坏瓜的比例为 $ p_2=\frac{2}{6} $ ； $ D_3 $ 包含样本 $ {5,11,12,14,16} $ ,其中类别为好瓜的比例 $ p_1=\frac{1}{5} $ ，坏瓜的比例为 $ p_2=\frac{4}{5} $ ,因此其三个分支点的信息熵为：\[ Ent(D_1) = - ( \frac{3}{6}\log_2\frac{3}{6} + \frac{3}{6}\log_2\frac{3}{6})=1.000 \] \[ Ent(D_2) = - ( \frac{4}{6}\log_2\frac{4}{6} + \frac{2}{6}\log_2\frac{2}{6})=0.918 \] \[ Ent(D_3) = - ( \frac{1}{5}\log_2\frac{1}{5} + \frac{4}{5}\log_2\frac{4}{5})=0.722 \]

2.2 信息增益（information gain）

  信息增益，由《统计学习方法》中定义：

特征 $ a $ 对训练数据集 $ D $ 的信息增益 $ Gain(D,a) $ ,定义为集合 $ D $ 的经验熵（即为熵）与特征 $ a $ 给定条件下的经验条件熵 $ Ent(D|a) $ 之差，即： \[ Gain(D,a)=Ent(D)-Ent(D|a) \]
其中特征 $ a $ 将数据集划分为： $ {D_1,D_2,...,D_v } $,而经验条件熵为： \[ Ent(D|a) = \sum_{i=1}^v \frac{\left|D_i\right|}{\left|D\right|}Ent(D_i)\]

  我们根据例子对其进行理解：
  对于特征“色泽”，我们计算其信息增益，由2.1中，集合 $ D $ 的熵为： $ Ent(D)=0.998 $ ，对于特征“色泽”的三个分支点的熵为： $ Ent(D_1)=1.000，Ent(D_2)=0.918，Ent(D_3)=0.722 $，则“色泽”特征的信息增益为：
\[ Gain(D,色泽)=Ent(D)-\sum_{i=1}^3 \frac{\left|D_i\right|}{\left|D\right|}Ent(D_i) = 0.998-(\frac{6}{17}\times1.000 + \frac{6}{17}\times0.918 + \frac{5}{17}\times0.722) = 0.109 \]

2.3 算法步骤

  ID3算法递归地构建决策树，从根节点开始，对所有特征计算信息增益，选择信息增益最大的特征作为节点的特征，由该特征的不同取值建立子节点；再对子节点递归地调用以上方法构建决策树；知道所有特征的信息增益均很小或者没有特征可以选择为止。最后得到一个决策树。

  在算法中（C4.5也是），有三种情形导致递归返回：

  （1）当前节点包含的样本全属于同一类别，无需划分。
  （2）当前属性集为空，或是所有样本在所有属性上取值相同，无法划分。（此时将所含样本最多的类别设置为该叶子节点类别）
  （3）当前节点包含的样本集合为空，不能划分。（将其父节点中样本最多的类别设置为该叶子节点的类别）

---

  输入：训练数据集 $ D $ ,特征集 $ A $ , 阈值 $ \epsilon $ ;
  过程：函数 $ TreeGenerate(D,A) $ .
  1：计算节点信息增益 $ Gain(D,a) $ :
  2：  节点a的熵： $ Ent(D,a) $
  3：  节点D的熵： $ Ent(D) $
  4：  节点信息增益： $ Gain(D,a)=Ent(D)-Ent(D,a) $
  5：生成节点node:
  6：if $ D $ 中样本全属于同一类别 $ C $ then
  7：  将node标记为 $ C $ 类叶节点；return
  8：end if
  9：if $ A = \emptyset $ OR $ D $ 中样本在 $ A $ 上取值相同then
  10：  将node标记为叶节点，期类别标记为 $ D $ 中样本数最多的类；return
  11：end if
  12：按照节点信息增益，从 $ A $ 中选择最优划分属性 $ a_* $
  13：for $ a_* $ 中的每一个值 $ a_* ^i $ do
  14：  为node生成一个分支；令 $ D_i $ 表示 $ D $ 中在 $ a_* $ 上取值为 $ a_* ^i $ 的样本子集；
  15：  if $ D_i $ 为空，then
  16：    将分支节点标记为叶节点，其类别标记为 $ D $ 中样本最多的类；return
  17：  else
  18：    以 $ TreeGenerate(D_i,A / { a_* }) $ 为分支节点
  19：  end if
  20：end for
  输出：以node为根节点的一棵决策树

---

---

3. C4.5算法

  实际上，信息增益准则对可取值书目较多的属性有所偏好，例如如果将前面表格中的第一列ID也作为特征的话，它的信息增益将达到最大值，而这样做显然不对，会造成过拟合。为了减少这种偏好可能带来的不利影响，C4.5算法中将采用信息增益比来进行特征的选择。信息增益比准则对可取值数目较少的属性有所偏好。接下来，我们首先对信息增益比进行介绍。

3.1 信息增益比（增益率）

  信息增益比的定义为： \[ Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)} \]，
  其中：\[ IV(a)=-\sum_{i=1}^v \frac{\left|D_i\right|}{\left|D\right|} \log_2\frac{\left|D_i\right|}{\left|D\right|} \]
  我们根据例子对其进行理解：

  对于特征“色泽”，我们计算其信息增益比，由2.2计算得 $ Gain(D,色泽)= 0.109 $，而 \[ IV(色泽)= -(\frac{6}{17}\times\log_2\frac{6}{17} + \frac{6}{17}\times\log_2\frac{6}{17} + \frac{5}{17}\times\log_2\frac{5}{17})=1.580 \]
  则 $ Gain\_ratio(D,色泽)=\frac{0.109}{1.580}=0.069 $。

3.2 算法步骤

  C4.5算法同ID3算法过程相似，仅在选择特征时，使用信息增益比作为特征选择准则。

---

  输入：训练数据集 $ D $ ,特征集 $ A $ , 阈值 $ \epsilon $ ;
  过程：函数 $ TreeGenerate(D,A) $ .
  1：计算节点信息增益比 $ Gain_ratio(D,a) $ :
  2：  节点a的熵： $ Ent(D,a) $
  3：  节点D的熵： $ Ent(D) $
  4：  节点信息增益： $ Gain(D,a)=Ent(D)-Ent(D,a) $
  5：  节点固定值： $ IV(a) $
  6：  节点信息增益比： $ Gain _ ratio(D,a)= \frac{Gain(D,a)}{IV(a)} $
  7：生成节点node:
  8：if $ D $ 中样本全属于同一类别 $ C $ then
  9：  将node标记为 $ C $ 类叶节点；return
  10：end if
  11：if $ A = \emptyset $ OR $ D $ 中样本在 $ A $ 上取值相同then
  12：  将node标记为叶节点，期类别标记为 $ D $ 中样本数最多的类；return
  13：end if
  14：按照节点信息增益，从 $ A $ 中选择最优划分属性 $ a_* $
  15：for $ a_* $ 中的每一个值 $ a_* ^i $ do
  16：  为node生成一个分支；令 $ D_i $ 表示 $ D $ 中在 $ a_* $ 上取值为 $ a_* ^i $ 的样本子集；
  17：  if $ D_i $ 为空，then
  18：    将分支节点标记为叶节点，其类别标记为 $ D $ 中样本最多的类；return
  19：  else
  20：    以 $ TreeGenerate(D_i,A / {a_* }) $ 为分支节点
  21：  end if
  22：end for
  输出：以node为根节点的一棵决策树

---

---

4. 剪枝处理

  针对于在第1部分提到的最后一个问题：当训练数据量大、特征数量较多时构建的决策树可能很庞大，这样的决策树用来分类是否好？答案是否定的。决策树是依据训练集进行构建的，当决策树过于庞大时，可能对训练集依赖过多，也就是对训练数据过度拟合。从训练数据集上看，拟合效果很好，但对于测试数据集或者新的实例来说，并不一定能够准确预测出其结果。因此，对于决策树的构建还需要最后一步----即决策树的修剪。
  决策树的修剪，也就是剪枝操作，主要分为两种：
  （1）预剪枝（Pre-Pruning）
  （2）后剪枝（Post-Pruning）
  接下来我们将详细地介绍这两种剪枝方法。

4.1 预剪枝（Pre-Pruning）

  预剪枝是指在决策树生成过程中，对每个节点在划分前先进行估计，若当前节点的划分不能带来决策树泛化性能的提升，则停止划分并将当前节点标记为叶节点。
  我们使用例子进一步理解预剪枝的过程：
  将本文开始的西瓜数据集表划分成两部分，一部分作为训练集用来构建决策树，一部分作为验证集用来进行决策树的剪枝。具体划分见下图：

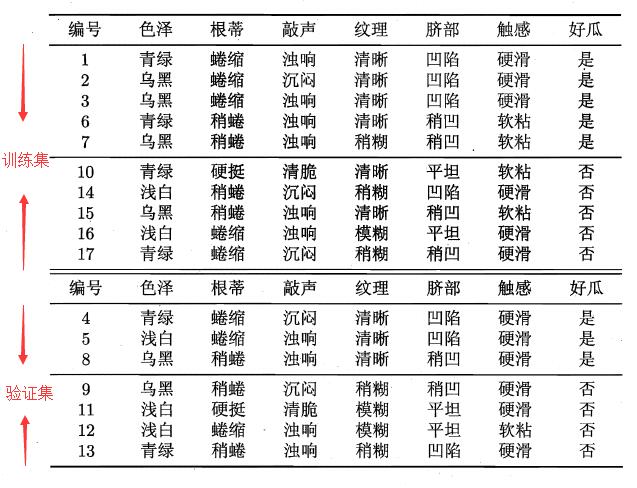
  使用ID3算法进行决策树的构建，即使用信息增益进行特征的选择。首先选择特征“脐部”作为决策树根节点，如何判断该节点是否需要剪枝，需要对剪枝前后验证集精度进行比较。由“脐部”这个特征将产生三个分支“凹陷”、“稍凹”、“平坦”，并认定其分支结果（可采用多数表决法，当分类数量相当时，任选一类即可），如下图：

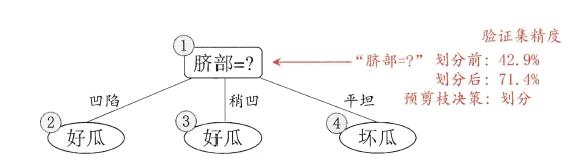
  查看验证集，若将“脐部”看做节点，并将其标记为“好瓜”，那么划分前的精度为： $ \frac{3}{7} = 0.714 $。符合“脐部”=“凹陷”的样本有： $ {4,5,13} $ ，其中正样本（是好瓜）为 $ {4,5} $ ，正样本个数为2，按照上图预测正确数为2；同理“脐部”=“稍凹”的样本中正样本个数为1，预测正确数为1；“脐部”=“平坦”的样本中负样本个数为2，预测正确个数为2。因此使用“脐部”这个特征进行划分，划分后的精度为： $ \frac{5}{7} = 0.714 $。由于预测后精度大于预测前精度，因此不对“脐部”进行剪枝，即将其作为划分点进行划分。

  同理我们“色泽”以及“根蒂”特征进行划分前后精度的计算。对于“色泽”，划分后的精度为 $ 0.571 $ ，而划分前为 $ 0.714 $ ，划分使得结果变差，因此不以该特征进行划分，即将该节点记为叶子节点并标记为“好瓜”；同理“根蒂”特征划分前后的精度都为 $ 0.714 $ ，效果并未提升，因此也不将该特征进行划分，而是将其作为叶子节点并标记为“好瓜”。由此，决策树构建完毕。此时的决策树为只有一层的树。

  可有由图中看出，该决策树有点过于简单，虽然降低的过拟合的风险，但是由于其基于“贪心”的本质禁止了其它分支的展开，给预剪枝决策树带来了欠拟合的风险。

4.1 后剪枝（Post-Pruning）

  后剪枝是指先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察，若将该节点对应的子树替换为叶节点能带来决策能力的提升，则将该子树替换成叶节点。
  我们使用例子进一步理解后剪枝的过程：
  同样适用4.1中的划分数据集。针对已建立好的决策树，我们首先对“纹理”特征节点进行处理，判断其是否需要剪枝，见下图。

  首先，使用整个决策树对验证集进行预测，并将其预测结果与真实结果进行对比，可得到如下结果（预测结果与真实结果相同，标记为“正确”，否则标记为“不正确”）：\[ \{(4,正确),(5,不正确),(8,不正确),(9,不正确),(11,正确),(12,正确),(13,不正确)\} \]
  首先我们判断是否需要对“纹理”进行剪枝：剪枝前精确度由上结果可以得到为 $ \frac{3}{7} = 0.429 $ ,剪枝后（即将该节点标记为“好瓜”），此时对于样本 $ {((8,正确))} $ ，其它样本结果不变，其精度提升到 $ \frac{4}{7} = 0.571 $ ，因此对该节点进行剪枝。对节点5“色泽”，剪枝前精确度为 $ 0.571 $ ，剪枝后仍旧为 $ 0.571 $ ，对此我们可以不进行剪枝（但在实际情况下仍旧会需要剪枝）；同理对“根蒂”、节点2“色泽”进行计算，所得结果见上图。由此得到后剪枝决策树。

  后剪枝决策树通常比预剪枝决策树保留了更多的分支，一般情况下，后剪枝决策树欠拟合的风险很小，其泛化能力往往优于预剪枝预测数。但由于其是基于创建完决策树之后，再对决策树进行自底向上地剪枝判断，因此训练时间开销会比预剪枝或者不剪枝决策树要大。

---

引用及参考：
[1]《机器学习》周志华著
[2]《统计学习方法》李航著
[3]《机器学习实战》Peter Harrington著

写在最后：本文参考以上资料进行整合与总结，属于原创，文章中可能出现理解不当的地方，若有所见解或异议可在下方评论，谢谢！
若需转载请注明：http://www.cnblogs.com/lliuye/p/9008901.html