[ABC305C] Snuke the Cookie Picker题解

题目大意

有一个 \(H\times W\) 的网格，一种有一个矩形，矩形中间有一个点被挖空，求这个点的坐标。（. 表示空白，# 表示矩形内的点）

解析

观察我们可以发现，每一矩形内的个点上下左右至少会有两个是 #。

如图：

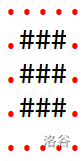
而每一个在矩形外的点上下左右最多只有一个 #。

所以我们只需要找的一个 . 的上下左右有两个及以上的 # 即可。

具体细节请看代码

Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
char a[1000][1000];
int n,m,s;
int x,y;
signed main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			cin>>a[i][j];

	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(a[i][j]=='.'){//如何只是一个空点
				int sum=0;
				if(a[i][j-1]=='#') sum++;//判断上下左右的 # 数量
				if(a[i-1][j]=='#') sum++;
				if(a[i][j+1]=='#') sum++;
				if(a[i+1][j]=='#') sum++;
				if(sum>=2){//找到了这个点
					cout<<i<<" "<<j;
					return 0;
				}
			}
	return 0;
}