LeetCode 周赛 348（2023/06/05）数位 DP 模板学会了吗

本文已收录到 AndroidFamily，技术和职场问题，请关注公众号 [彭旭锐] 加入知识星球提问！

• 往期回顾：LeetCode 单周赛第 347 场 · 二维空间上的 LIS 最长递增子序列问题

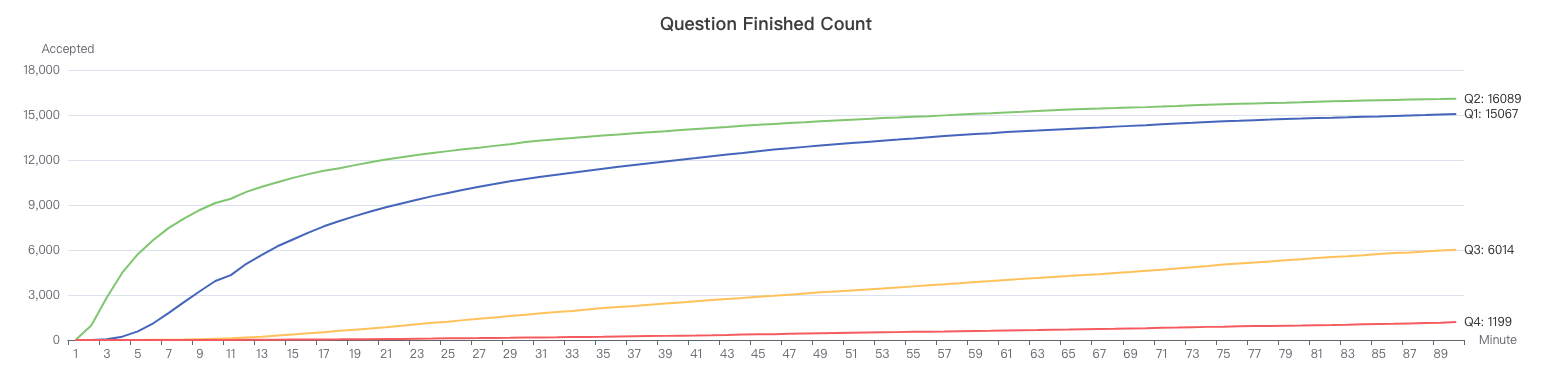
周赛 348 概览

T1. 最小化字符串长度（Medium）

• 标签：散列表、计数

T2. 半有序排列（Easy）

• 标签：散列表

T3. 查询后矩阵的和（Medium）

• 标签：散列表

T4. 统计整数数目（Hard）

• 标签：数位 DP、构造

---

T1. 最小化字符串长度（Medium）

https://leetcode.cn/problems/minimize-string-length/

题解（散列表 + 计数）

无论每个字符有多少，最终每个字符都会剩下 1 个，因此只需要记录字符种类数：

class Solution {
    fun minimizedStringLength(s: String): Int {
        return s.toHashSet().size
    }
}

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

---

T2. 半有序排列（Easy）

https://leetcode.cn/problems/semi-ordered-permutation/

题解（模拟）

我们只需要考虑 1 和 n，每次操作可以把 1 向左边移动一位，或者将 n 向右移动一位，但是考虑到 1 和 n 的移动方向有交叉时，要减少一次操作次数。

class Solution {
    fun semiOrderedPermutation(nums: IntArray): Int {
        val n = nums.size
        val i = nums.indexOf(1)
        val j = nums.indexOf(n)
        return i + (n - 1 - j) - if (i > j) 1 else 0
    }
}

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

---

T3. 查询后矩阵的和（Medium）

https://leetcode.cn/problems/sum-of-matrix-after-queries/

题解（散列表）

这道题需要一点逆向思维，越靠后的操作会覆盖越靠前的操作，所以我们逆序遍历，并维护：

• rowSet：操作过的行号（逆序）
• colSet：操作过的列号（逆序）

那么，在每次行操作中可以填充的次数就是该行中没有被操作过的列数，而每次行操作中可以填充的次数就是该列中没有被操作过的行数。

class Solution {
    fun matrixSumQueries(n: Int, queries: Array<IntArray>): Long {
        var ret = 0L
        val visitSet = Array(2) { HashSet<Int>() }
        for (query in queries.reversed()) {
            val type = query[0]
            val index = query[1]
            val value = query[2]
            // 重复操作
            if (visitSet[type].contains(index)) continue
            // 这次操作可以填充的数字
            ret += 1L * (n - visitSet[type xor 1].size) * value
            visitSet[type].add(index)
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(q)$
• 空间复杂度：$O(n + q)$

---

T4. 统计整数数目（Hard）

https://leetcode.cn/problems/count-of-integers/

题解（数位 DP）

1、定义 f(n) 表示 [1,n] 中满足条件的好整数，那么原问题的解为：f(num2) - f(num1) + if(num1)

2、使用数位 DP：

以 n = 234 为例

• isLimit：高位是否约束当前位。例如百位填 2 时，十位就受到高位约束只能填 0-3，否则可以填 0-9
• isNum：高位是否为数字，这题不要考虑前导 0

3、定义 dfs(i:Int, sum:Int, isLimit:Int) 表示子问题中满足条件的个数

4、在备忘录中，isLimit 为 true 的子问题只会递归 1 次，可以不为 isLimit 提供记忆化维度：

class Solution {

    private val MOD = 1000000007

    fun count(num1: String, num2: String, min_sum: Int, max_sum: Int): Int {
        return count(num2, min_sum, max_sum) - count(num1, min_sum, max_sum) + check(num1, min_sum, max_sum)
    }

    private fun check(num: String, min_sum: Int, max_sum: Int): Int {
        var sum = 0
        for (c in num) sum += c - '0'
        return if (sum in min_sum..max_sum) 1 else 0
    }

    // 数位 DP
    private fun count(num: String, min_sum: Int, max_sum: Int): Int {
        fun dfs(num: String, memo: Array<IntArray>, i: Int, sum: Int, isLimit: Boolean): Int {
            // 终止条件
            if (sum > max_sum) return 0
            if (i == num.length) return if (sum >= min_sum) 1 else 0
            // 备忘录
            if (!isLimit && memo[i][sum] != -1) return memo[i][sum]
            // 上界
            val upper = if (isLimit) num[i] - '0' else 9
            var ret = 0
            for (choice in 0 .. upper) {
                ret = (ret + dfs(num, memo, i + 1, sum + choice , isLimit && choice == upper)) % MOD
            }
            // 备忘录
            if (!isLimit) memo[i][sum] = ret
            return ret
        }

        val n = num.length
        val m = Math.min(9 * n, max_sum) + 1
        return dfs(num, Array(n) { IntArray(m) { -1 } }, 0, 0, true)
    }
}

复杂度分析：

• 时间复杂度：$O(10·n·m)$
• 空间复杂度：$O(n·m)$

---

往期回顾

• LeetCode 单周赛第 347 场 · 二维空间上的 LIS 最长递增子序列问题
• LeetCode 单周赛第 346 场 · 仅 68 人 AK 的最短路问题
• LeetCode 双周赛第 104 场 · 流水的动态规划，铁打的结构化思考
• LeetCode 双周赛第 103 场 · 区间求和的树状数组经典应用