hdu-4471-Homework-矩阵快速幂+优化加速

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=4471

题目意思：

求f(n).

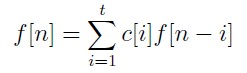
当n为特殊点nk时

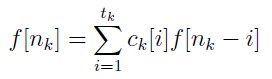
解题思路：

当x不为特殊点时，直接用基本的矩阵快速幂，求出f[x],当x为特殊点时，用另外一个矩阵，左乘转移一下。

也就是按特殊点nk,将1-n分成很多区段，一个区段一个特殊点这样来回求。

两点优化：

1、因为要多次用到同一矩阵的快速幂，所以先预处理该矩阵的2K次幂，免的计算每个区间的时候，都要计算该矩阵的2K次幂。

2、矩阵相乘的时候，把K作为主要控制元，一次计算 a[i][k]*a[k][j] ,当有a[i][k]等于0时，直接跳出来。

注意：

矩阵大小的选取，位置的选放。

c1 c2 c3 ... ct    f(n-1)                  f(n)

1  0   0   ... 0     f(n-2)                  f(n-1)

0  1   0   ... 0     f(n-3)                  f(n-2)

0  0   1   ... 0     ...                        ...

...   ....     ... .       ...                       ...

0  0   0  ..1 0     f(n-t)                  f(n-t+1)

话不多说。

代码解释的很详细：

#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<stack>
#include<list>
#include<queue>
#define eps 1e-6
#define INF 0x1f1f1f1f
#define PI acos(-1.0)
#define ll __int64
#define lson l,m,(rt<<1)
#define rson m+1,r,(rt<<1)|1
using namespace std;
#define Maxn 110
#define M 1000000007

/*
freopen("data.in","r",stdin);
freopen("data.out","w",stdout);
*/

//本题基本思路不难想到，主要是细节优化
//学习简洁写法

struct Mar
{
   int row,col;
   int s[Maxn][Maxn];

   void init(int a,int b)
   {
      row=a,col=b;
      memset(s,0,sizeof(s));
   }
};

Mar operator * (const Mar & a,const Mar & b)
{
   Mar res;
   res.init(a.row,b.col); //初始化

   for(int k=1;k<=a.col;k++) //以列向量为标准，在0较多的情况下可以降低时间复杂度，
   {                         //以后注意这样写
      for(int i=1;i<=res.row;i++)
      {
         if(a.s[i][k]==0)
            continue;
         for(int j=1;j<=res.col;j++)
         {
            if(b.s[k][j]==0)
               continue;
            res.s[i][j]=(1LL*a.s[i][k]*b.s[k][j]+res.s[i][j])%M; //枚举k时，想成可能为0
         }  //强制转化为ll类型，免得超了
      }
   }
   /*
   for(int i=1;i<=res.row;i++)
      for(int j=1;j<=res.col;j++)
         for(int k=1;k<=a.col;k++)
            res.s[i][j]=(1LL*a.s[i][k]*b.s[k][j]+res.s[i][j])%M;*/
   return res;
}

Mar ba,sp[Maxn],ans,pp[35]; //pp[i]表示ba^(2*i)是预处理的矩阵,免得每一次都要计算
int nn[Maxn],tt[Maxn],m,n,q,t,pos[Maxn];//对下表排序

void getpp()
{
   pp[0]=ba;
   for(int i=1;i<=31;i++) //10^9 最多也就2^31次方
      pp[i]=pp[i-1]*pp[i-1];
}

bool cmp(int a,int b) //对下标排序，免得每次都移动，特别是单个元素内容很多时，浪费时间
{
   return nn[a]<nn[b];
}

void Cal(int a)//a表示次数,矩阵快速幂算,另外一种写的形式
{
   for(int i=0;i<=31;i++)
   {
      if(a&(1<<i))
         ans=pp[i]*ans;
   }
   return ;
}
/*
void Cal(int a) //这样写就tle,因为每个区段都要重新算矩阵的次方，果断采用上面的那种思路
{
   Mar tmp=ba;
   while(a)
   {
      if(a&1)
         ans=tmp*ans;
      a=a>>1;
      tmp=tmp*tmp;
   }
}*/

int main()
{
   int ca=0;

   while(scanf("%d%d%d",&n,&m,&q)!=EOF)
   {
      memset(ans.s,0,sizeof(ans));
      for(int i=m;i>=1;i--)
         scanf("%d",&ans.s[i][1]); //开始的m个
      scanf("%d",&t);
      memset(ba.s,0,sizeof(ba.s));
      for(int i=1;i<=t;i++)  //
         scanf("%d",&ba.s[1][i]);
      //scanf("%d",&q);
      for(int i=1;i<=q;i++)
      {
         pos[i]=i;
         scanf("%d%d",&nn[i],&tt[i]);
         memset(sp[i].s,0,sizeof(sp[i].s));
         for(int j=1;j<=tt[i];j++)
            scanf("%d",&sp[i].s[1][j]);
      }
      int Max=t;
      for(int i=1;i<=q;i++)
         Max=max(Max,tt[i]); //把最大的表长找到
      ba.row=ba.col=Max;
      ans.row=Max,ans.col=1;
      for(int i=2;i<=ba.row;i++) //构造基本的矩阵
         ba.s[i][i-1]=1;

      getpp();

      for(int i=1;i<=q;i++)
      {
         sp[i].row=sp[i].col=Max;
         for(int j=2;j<=sp[i].row;j++) //构造特殊位置的矩阵
            sp[i].s[j][j-1]=1;
      }
      sort(pos+1,pos+1+q,cmp); //由下标对nn排序

      int last=m;
      for(int i=1;i<=q;i++)
      {
         int p=pos[i]; //定位

         if(nn[p]>n||nn[p]<=last) //不用算
            continue;
         Cal(nn[p]-last-1);
         ans=sp[p]*ans; //特殊点单独计算
         last=nn[p];
      }
      Cal(n-last);
      printf("Case %d: %d\n",++ca,ans.s[1][1]);

   }

   return 0;
}