Codeforces Round #277 (Div. 2)

整理上次写的题目：

A:

For a positive integer n let's define a function f:

f(n) =  - 1 + 2 - 3 + .. + ( - 1)nn

Your task is to calculate f(n) for a given integer n.

Input

The single line contains the positive integer n (1 ≤ n ≤ 10^15).

题目简洁。可以看出规律。。。分下奇偶就可以了。

B：

B. OR in Matrix

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's define logical OR as an operation on two logical values (i. e. values that belong to the set {0, 1}) that is equal to 1 if either or both of the logical values is set to 1, otherwise it is 0. We can define logical OR of three or more logical values in the same manner:

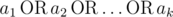 where 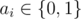 is equal to 1 if some ai = 1, otherwise it is equal to 0.

Nam has a matrix A consisting of m rows and n columns. The rows are numbered from 1 to m, columns are numbered from 1 to n. Element at row i (1 ≤ i ≤ m) and column j (1 ≤ j ≤ n) is denoted as Aij. All elements of A are either 0 or 1. From matrix A, Nam creates another matrix B of the same size using formula:

.

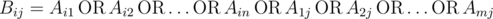(Bij is OR of all elements in row i and column j of matrix A)

Nam gives you matrix B and challenges you to guess matrix A. Although Nam is smart, he could probably make a mistake while calculating matrix B, since size of A can be large.

Input

The first line contains two integer m and n (1 ≤ m, n ≤ 100), number of rows and number of columns of matrices respectively.

The next m lines each contain n integers separated by spaces describing rows of matrix B (each element of B is either 0 or 1).

Output

In the first line, print "NO" if Nam has made a mistake when calculating B, otherwise print "YES". If the first line is "YES", then also print mrows consisting of n integers representing matrix A that can produce given matrix B. If there are several solutions print any one.

题目比较烦。

但是我们可以得出这样一个规律：先预设定所有数为1，然后按得出的答案去把数变为0.然后验证是否满足答案。。

明白这一点 就简单了。

 #include<iostream>
 #include<cmath>
 #include<cstdio>
 #include<vector>
 #include<string>
 typedef long long ll;
 using namespace std;

 int a[][];
 int b[][];
 int main()
 {
     int m,n;
     cin>>m>>n;
     for (int i=;i<=m;i++)
     for (int j=;j<=n;j++) b[i][j]=;
         for (int i=;i<=m;i++)
         for (int j=;j<=n;j++)
         cin>>a[i][j];

         for (int i=;i<=m;i++)
         for (int j=;j<=n;j++)
         if (a[i][j]==){
         for (int k=;k<=n;k++)
         b[i][k]=;
             for (int k=;k<=m;k++)
             b[k][j]=;
             }

         for (int i=;i<=m;i++)
         for (int j=;j<=n;j++)
         if (a[i][j]==)
         {
             int tmp=;
             for (int k=;k<=n;k++)
             tmp|=b[i][k];
             for (int k=;k<=m;k++)
             tmp|=b[k][j];
             if (tmp==)
             {
                 cout<<"NO";
                 return ;
                }
             }

           cout<<"YES"<<endl;
            for (int i=;i<=m;i++){
             for (int j=;j<=n;j++)
             cout<<b[i][j]<<" ";
             cout<<endl;
         }
         return ;
 }

C：

 

同样很繁琐的题目，但是我们可以贪心之。

贪心策略：1，先计算字符串的一半值。。。比如abcbcc

对应的值应当是211112.我们发现对半分的字符串所需最少的步数是对称的。还有我们要计算出最少步数。这里具体见代码。

然后当p在左半部分是就只做左半部分。同理右半部份。。。我们不可能p<=(n+1）/2，去做右半部份。

然后抽象认为这样的题目:数组为1 2 3 0 2的数组。当p在某个位置时。求全部变为0最少的步数。。。

这里用贪心或者啥的。我用了一个比较巧的办法。

然后因为写的太繁琐。露了条件。。。一直WA。。真是菜

 #include<bits/stdc++.h>
 using namespace std;
 #define N 123456
 string s;
 int a[N];
 int n,p;

 int main()
 {
         cin>>n>>p;
         cin>>s;
         for (int i=;i<s.size();i++){
         int tmp1=abs(s[i]-s[n-i-]);
         int tmp2;
         if (s[i]>s[n-i-]) tmp2=abs(s[i]--s[n-i-]);
         else tmp2=abs(s[n-i-]-s[i]-);
         a[i+]=min(tmp1,tmp2);
     }

     int mid=(n+)/;
     int ans=0x3f3f3f;

     if (p<=mid)
     {
        int ans1=;
        int tmpp=p;
        for (int i=;i<=mid;i++)
        if (a[i])
        {
           ans1+=a[i];
           ans1+=abs(tmpp-i);
           tmpp=i;
           }
          ans=min(ans1,ans);

          ans1=;
          tmpp=p;
          for(int i=mid;i>=;i--)
          if (a[i])
          {
           ans1+=a[i];
           ans1+=abs(tmpp-i);
           tmpp=i;
          }
          ans=min(ans1,ans);
     }

     else
     {

        int ans1=;
        int tmpp=p;
        for (int i=mid+;i<=n;i++)
        if (a[i])
        {
           ans1+=a[i];
           ans1+=abs(tmpp-i);
           tmpp=i;
        }
          ans=min(ans1,ans);
          ans1=;
          tmpp=p;
         for(int i=n;i>mid;i--)
         if (a[i])
         {
           ans1+=a[i];
           ans1+=abs(tmpp-i);
           tmpp=i;
         }
         ans=min(ans,ans1);
     }

     cout<<ans<<endl;
     return ;
 }

D题：不是原创。

我们可以这样处理。

每次枚举第I个数。并且默认为根节点。且权值最大。然后我们的目的是找到多少个其子树是满足max-min<=d;

这里用DFS就好了。

 #include<bits/stdc++.h>
 #define N 12345
 #define mod 1000000007
 typedef long long ll;
 using namespace std;
 int a[N];
 int con;
 vector<int> mp[N];
 int d;

 ll dfs(int p,int pre)
 {
     ll tot=;
     for (int i=;i<mp[p].size();i++)
     {
         int v=mp[p][i];
         if (pre==v||a[con]<a[v]||a[con]-a[v]>d||(a[con]==a[v]&&v<con)) continue;
         tot=tot*(dfs(v,p)+)%mod;
     }
     return tot;
 }

 int main()
 {
     int n;
     cin>>d;
     cin>>n;
     for (int i=;i<=n;i++) cin>>a[i];
     for (int i=;i<n;i++)
     {
         int x,y;
         cin>>x>>y;
         mp[x].push_back(y);
         mp[y].push_back(x);
     }
     ll ans=;
     for (int i=;i<=n;i++)
     {
         con=i;
         ans=(ans+dfs(i,-))%mod;
     }
     cout<<ans;
 }

E:继续补...不出来了。。。

还是忍不住看了题解。。

先说说自己的想法好了。。

解析：如果我们用二分做LIS 会发现我们做的事“字典序最小的LIS"，怎么理解。。

比如 1 3 2 5.。我们会算出这样的3个数：1 2 5.

其实很多东西包含在这里。。

比如：我们预先算出每个数“对应多少个”。 比如 1 4 2 5 7 3 9

1 2 2 3 4 3 5

算出这样的数列

那么答案出来了 ai=4&&ai=2 是两个答案。 ai=5输出一种，ai=3不再LIS 里面。

然后代码就是这样了：

 #include<bits/stdc++.h>
 using namespace std;
 #define N 123456
 int a[N],b[N],c[N];
 int good[N];
 int dp[N];
 int now[N];

 int main()
 {
     int n;
     cin>>n;
     for (int i=;i<=n;i++) cin>>a[i];

     int t=;
     for (int i=;i<=n;i++)
     {
         if (a[i]>b[t]) {b[++t]=a[i];dp[i]=t;}
         else
         {
            int x=lower_bound(b+,b+t+,a[i])-b;
            b[x]=a[i];
            dp[i]=x;
         }
     }

     int mx=t;

     for (int i=n;i>=;i--)
     if (dp[i]==mx||now[dp[i]+]>a[i])
     {
         good[i]=dp[i];
         c[good[i]]++;
         now[dp[i]]=max(now[dp[i]],a[i]);
     }

     for (int i=;i<=n;i++)
     {
         if (c[good[i]]==) cout<<;
         else if (c[good[i]]==) cout<<;
         else cout<<;
     }
     return ;
 }