基于RRCF（robust random cut forest）的时间序列异常检测流程

摘要：RRCF是亚马逊提出的一个流式异常检测算法，是对孤立森林的改进，可对时序或非时序数据进行异常检测。本文是我从事AIOps研发工作时所做的基于RRCF的时序异常检测方案。

1.      数据格式

将时间序列以滑动窗口的形式转换为d维空间点。例如对于时间序列[1,2,3,4,5,6,7,8]，d=5，那么可以将该时间序列转换为4个空间点[(1,2,3,4,5),(2,3,4,5,6),(3,4,5,6,7),(4,5,6,7,8)]。RCF以这样的高维空间点进行建模和检测。

2.      参数

点的维度d；

森林里树的数量tree_num；

单棵树的大小tree_size，即一棵树中包含多少点；

异常阈值thresh，即根据RCF异常得分判定是否异常的阈值。

3.      RCF原理

3.1树的构建

输入：数据集S，数据的维度d。

输出：一个包含branch和leaf的树。

1. 计算每个维度上的跨度：
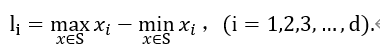
2. 维度选择：按照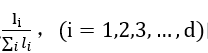的概率随机选择一个维度q.
3. 切分点选择：对维度q,按照均匀概率分布，随机选择该维度的一个切分点.
4. 维度q和对应切分点p构成一个branch.该branch将数据集S切分为两个子节点：；
5. 若或者集合中只有一个点，则将该子节点标记为这棵树的叶子节点（leaf）。
6. 若或者集合中的点的数量大于1，则重复迭代1~5步骤。直到所有的点都变为叶子节点（leaf）。

3.2点的删除和插入

可以证明（论文引理4、6）：

1、点的删除：将点p从由S构成的树T中删除，得到的树T’和直接从点集S-{p}构建的树T’’的概率分布是一致的。

2、点的插入：将点p插入到由S构成的树T中，得到的树T’和直接从点集S∪{p}构建的树T’’的概率分布是一致的。

这两个引理意味着，要计算点的加入和删除带来的树的复杂度的变化，只需要将点插入到原有的树中，或从原有的树中删除，而不需要使用新的点集重新构建树。这是RCF算法可用于流式检测的理论依据。

3.3异常得分codisp的计算

树的表示：树的每一个叶子节点都可以使用一个bit向量进行表示，如（0,0,1,0），0代表是父节点的左孩子，1代表是父节点的右孩子，同时向量的长度（即比特数）也就是该叶子节点在树中的深度。因此，一棵树可由所有叶子节点的bit向量来刻画。

树的复杂度：将树T的复杂度|M(T)|定义为，描述一棵树所需要的bit数。因此树的复杂度也等于所有叶子节点在树中的深度的和。

点的displacement：将一个叶子节点从树中删除，将导致树的结构发生改变，也会导致树的复杂度发生改变。将一个点删除后，树的复杂度的变化量（减少量）定义为该点的displacement。点的displacement表征了一个点的异常程度，displacement越大，该点越可能是异常。

点的co-displacement：displacement是计算删除一个点后树的复杂度的变化量，假如被删除的点是异常点，但如果树中还存和被删除点十分靠近的点，那么删除这个异常点将不会导致树的结构发生大的变化，因此其displacement就不会很大，因此很可能会把这个点误判为非异常点。这种现象在异常检测领域被称为masking。为解决masking问题，使用co-displacement作为点的异常评分。

在计算co-disp时，除了删除待检测目标点，还要考虑删除与目标点比较接近的点集，然后计算树的复杂度的变化量。

具体做法为（证明见引理2）：

从待检测的叶子节点出发，沿着叶子节点到根节点的路径，分别尝试删除该叶子节点、该叶节点的父、祖父、曾祖父……节点，每删除一个节点（也就是一个点集），计算模型复杂度的变化量。该叶子节点的co-disp定义为所有变化量的最大值。

异常检测：检测时，将待检测点插入到森林中的每一棵树中，计算所有树对该点的异常评分co-disp，取其平均值作为该点的异常得分。

4.      异常检测过程

4.1热启动

4.1.1模型训练

1. 将时间序列转化为空间点集S，且应保证|S|>=tree_num*tree_size；
2. 如果|S|>tree_num*tree_size，对S进行下采样至 |S|=tree_num*tree_size；
3. 对S进行分区，将其分为tree_num份，每份包含tree_size个点；
4. 使用S的每一个分区构建一棵树，所有的树构成一个森林。
5. 接收一个新点；
6. 对该点是否异常进行判定：

4.1.2异常检测过程

i.            将新点插入到每一棵树中，并计算每一棵树对该点的异常评分co-disp；

ii.            计算所有树的异常评分的均值作为该点的异常得分；

iii.            异常得分与异常阈值比较，进行异常判定；

iv.            将新点从每棵树中删除；

1. 将新点更新到模型中：

i.            随机选择一棵树；

ii.            将该树中最旧的点删除；

iii.            将新点插入该树；

4.2冷启动

也可以冷启动的方式运行，不事先训练模型，直接启动检测，为每个序列初始化一个模型（由若干空树构成的森林），随着数据的流入，树不断增长，直到达到设定的tree_size后，模型的大小不再改变，但仍然持续更新。这种工作方式可由引理6作支撑。过程类似：

a)       首先初始化tree_num棵空树；

b)      接收一个新点；

c)       对该点是否异常进行判定：

i.            将新点插入到每一棵树中，并计算每一棵树对该点的异常评分co-disp；

ii.            计算所有树的异常评分的均值作为该点的异常得分；

iii.            异常得分与异常阈值比较，进行异常判定；

iv.            将新点从每棵树中删除；

d)      将新点更新到模型中：

i.            随机选择一棵树；

ii.            如果树的大小已达到tree_size，则将该树中最旧的点删除，否则跳过；

iii.            将新点插入该树；