SLAM基础算法（1）：卡尔曼滤波

对于一个正在运动中的小车来说，如何准确的知道它所处的位置？

理论家说：我可以通过牛顿公式来计算！

实践家说：给它装个GPS不就得了！

好吧，你们说的听上去都很有道理，但我们到底该相信谁？

现实情况是：

理论家没有考虑到现实存在的摩擦力、空气阻力、时间测量误差等因素，算出来的结果存在较大误差；

实践家没有考虑GPS的测量存在较大误差。

这样一说，感觉两位半斤八两，都有误差，感觉谁都不可信。不过，我们还是要解决问题的嘛，能不能让这两位合作一下呢，理论联系实际嘛，马克思他老人家说的准没错。

我们知道，误差其实是一种噪声，那么是不是可以用滤波的方法呢？

感觉可以，我们把他俩的结果加起来，再除二嘛，均值滤波谁不会呢！但是，但是传感器的测量值（不一定是GPS）有时候简直会上天哪，这样简单粗暴肯定不靠谱，那有没有更牛X的方法呢？

-------------------------------------------------------------------------------------------------严肃的分隔线----------------------------------------------------------------------------------------

在刚刚提出的例子里，小车的状态向量可以表示为：

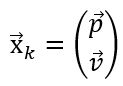
这时候，理论家提出，他可以预测k时刻的小车状态，并很难受的承认，这个预测是有误差的，假设这个误差服从正态分布：

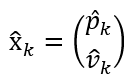
给出误差的协方差矩阵

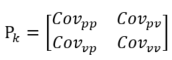
假设小车是匀速行驶，使用基本的运动学公式来表示，有：

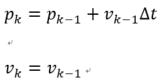
即：

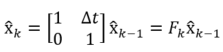
其中：

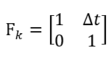
称为预测矩阵。

现实中，小车肯定不是匀速的，因为各种阻力的存在，需要时不时的给小车一个向前的力，才能使它继续向前行驶：

假设某个时刻给了小车一个向前的力，产生了一个向前的加速度a，那么：

即：

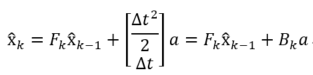
其中：

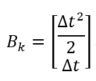
称为控制矩阵。

对于施加给小车的加速度a，它也称为一个向量，叫做控制向量，常用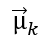来表示，即有：

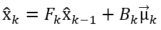
到这里，理论家的事情也差不多了，我们为他补上最后一步。在系统会中，可能会有其他不可预知的外力可能会干扰预测结果，我们需要把这一部分误差也加进来，假设它也是一个服从正态分布的误差，我们已经知道：

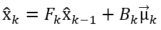
则有：

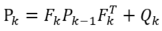
可以看出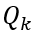，是有上一步得来的外部不确定性误差的总和。

这时，实践家也给出了他买的山寨GPS的参数，知道了这个GPS的误差范围，那么有如下关系：

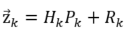
其中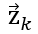， 为观测向量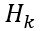， 为传感器与现实单位换算的转换矩阵（这里因为GPS输出单位与现实一致，就是1：1的关系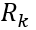）， 为GPS的正态分布协方差矩阵。

OK，到现在为止，理论和实践的要素都准备完成，是时候把他们整在一起了，我们先来看一幅图片：

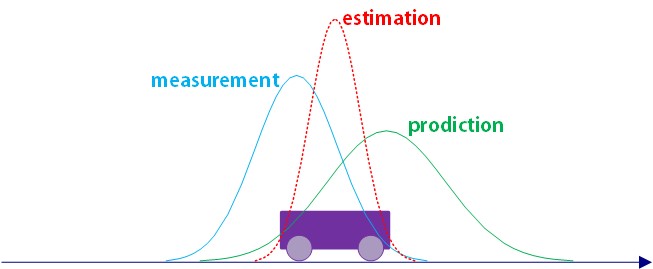
图中紫色的小车正在行走，理论家计算出的位置为绿色曲线（正态分布），实践家测量出的位置为蓝色曲线（也是正态分布），那么我们如果把这两个正态分布融合起来，是不是得出一个更“瘦”的曲线呢？

如上图红色所示，我们得出了融合后的曲线，这个曲线的方差要比另外两个要小了，至于为啥高斯分布和高斯分布融合起来还是高斯分布，请参考论文《Products and Convolutions of Gaussian Probability Density Functions》有详细的推导和论证，这里就不多说啦。

现在，我们有了两个不同的数据集，分别是预测的数据和测量的数据，我们用 来归一到相同的单位，则有：

稍微加以变形，不难得出：

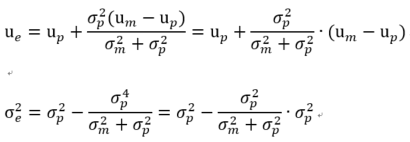
设：

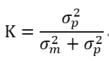
那么上面的公式变为：

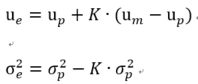
代入：

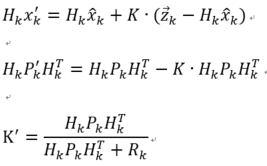
为了得到最后的结果，把上面三个式子化简，最终得到：

总结一下，我们把卡尔曼滤波的过程一般分为两大部分，预测更新和测量更新：

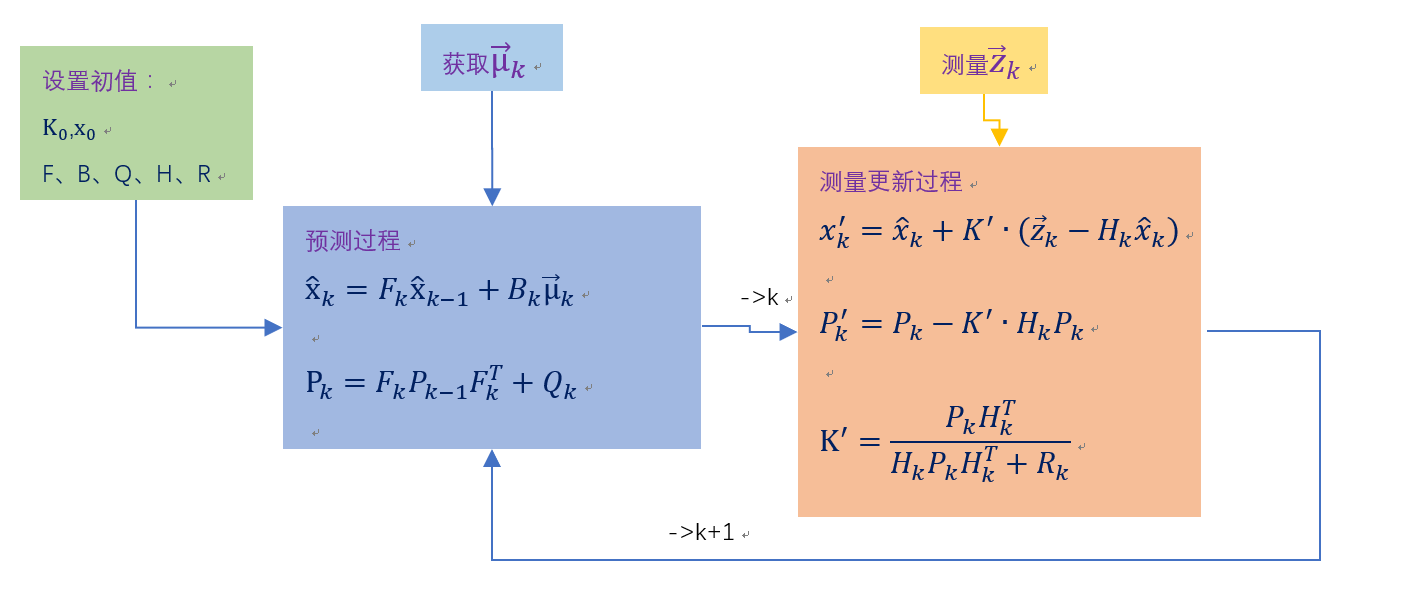
到这里，了解了卡尔曼滤波大概的推理和机制，说白了，卡尔曼滤波就是通过不断的迭代，将测量结果不断收敛的一种方法。可能到这里我们还是不太明白卡尔曼滤波有啥牛X的，那我们接下来具体计算一下。

以小车的运动为例，为了简化运算假设它是匀速行驶，我们每隔1秒获取一次GPS的数据并算出相对位移，数据如下：

此时，由上述条件容易得知：

1） 由于是匀速行驶，所以不需要控制量，可以忽略；

2） 1秒一次的更新间隔，预测矩阵F，这里是预测因子为1；

3） GPS输出的测量数据已转换为和现实一致，故H=1；

4） 假设小车初速为0，方差为1；

5） 就上面说的，GPS的误差是R=1米

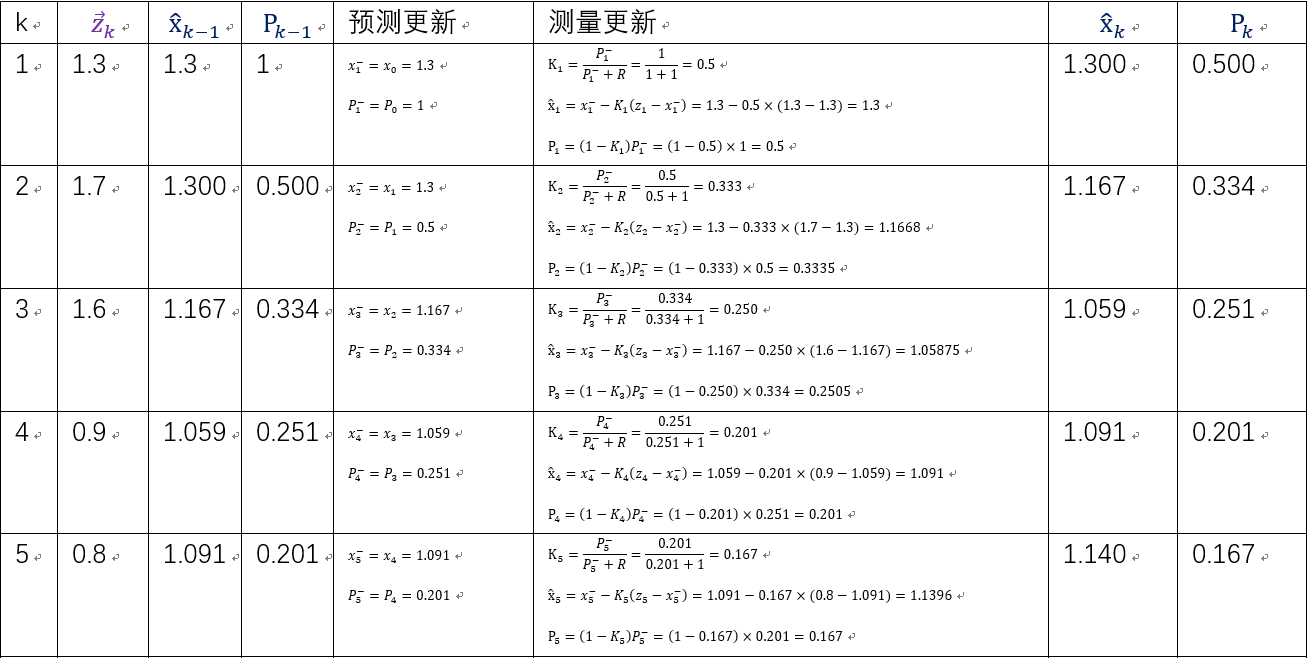
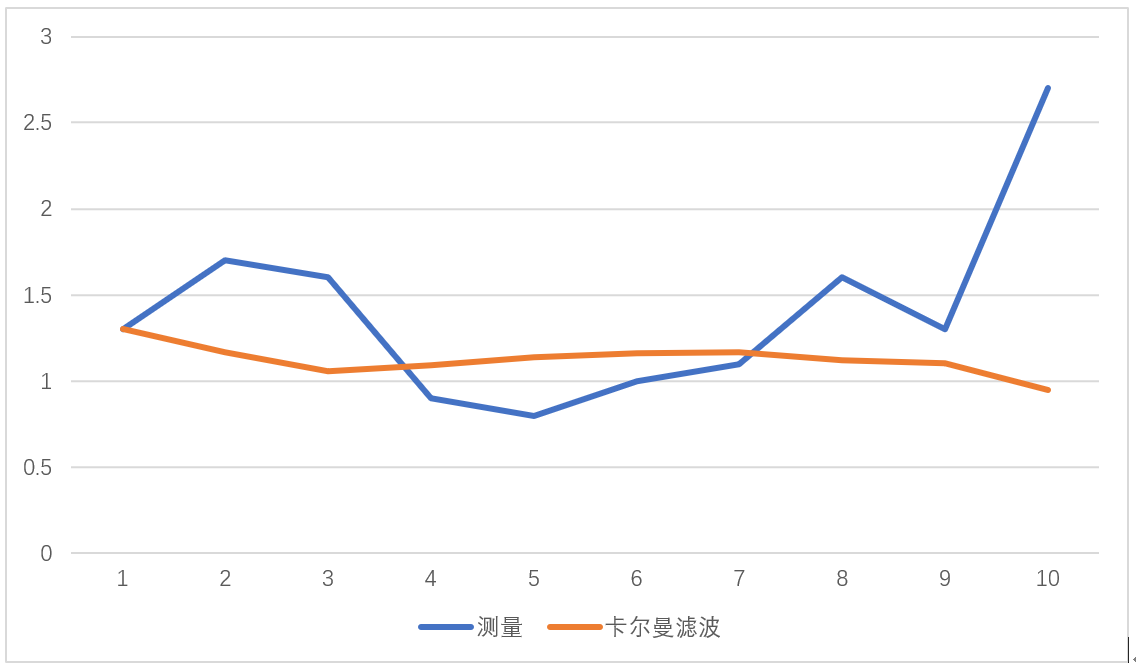
可以看出，滤波后的结果相比测量的结果，是比较收敛的，接近于小车匀速运动的现实情况。

References:

[1]"A New Approach to Linear Filtering and Prediction Problems" by R.E.Kalman,1960

[2]"Kalman filter" in wikipedia

[3]"How a Kalman filter works,in pictures" by Bzarg's blog

[4]《Probabilistic Robotics》