Andrew Ng机器学习算法入门(八):正规方程

正规方程

在先学习正规方程之前，先来复习一下之前学过的常规的回归方程的解法。

假设存在如果的代价函数，

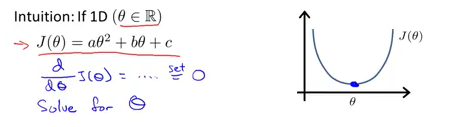
，解法也十分的简答。

但是有时候遇到的情况或许会变得相当的复杂。

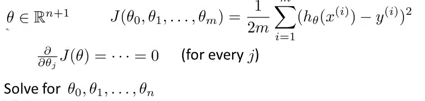
的数，如果是按照常规的方式进行求解，那么按照之前的求解方式，就需要对每一个theta进行微分，然后综合求最小值,这样的运算结果可能最后是相当的复杂。

那么这个时候正规方程就非常有用了。

正规方程对于theat的求解非常的简单，如下：

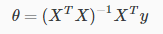
如何求解theta，

还是房价的例子，在房价中，假设房价与房屋面积，房间数量，房间位于的楼层，房间的年限有关，最终得到的训练数据如下：

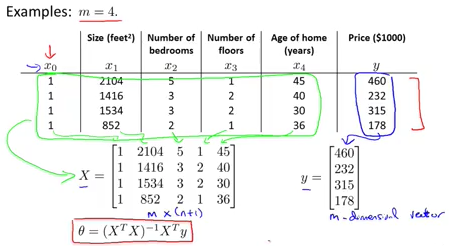
最后求得的theta的结果为：

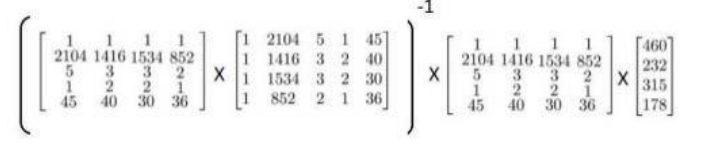
当的简单

正规方程与梯度下降算法的比较

由于使用markdwon不是很好画图，这里就直接使用列表的方式来显示了。

梯度下降算法的优缺点

• 需要选择学习率a
• 需要进行多次迭代
• 当特征(n)非常多时，算法效果很好
• 适用于各种类型的模型

正规方程算法的优缺点

• 不需要学习率
• 不需要进行迭代
• 需要计算转置、逆矩阵等算法
• 不适用于n比较大的情况，当n<10000时，还可以接受
• 仅仅适用于线性模型，不适合逻辑回归等其他的分类模型

总体来说，当特征数量不是很大的时候(小于10000)，标准方程是一个很好的计算参数theta的替代方法。

其他

有一点需要注意的时候，在使用正规方程的时候，需要计算

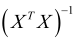
么就是否意味着无法进行下去了？

在Octave中，正规方程的写法是：

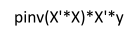
inv()方法还是能够处理。当然这种处理方式其实上还是借助于第三方的计算工具解决问题。

如果在计算机中真的出现了不可逆的举证，有可能是一下两种情况：

• 重复的特征，例如在房价的例子中，存在两个房屋面积的特征x1和x2。x1的单位是英尺，x2的单位是平方米。英尺和米是可以相互转换的，这样就导致这两个特征有一个是重复多余，这样就有可能导致不可逆。处理方法也很简单，直接去掉一个即可。
• 过多的特征，特征的数量n大于样本数量m。例如样本数量只有10个，但是特征数量有100个，这样也有可能会导致不可逆。处理的方式也很简单，删除一些特征或者是使用正规化的线性代数的方法。

为了了能到远方，脚下的每一步都不能少