神经网络与机器学习 笔记—Rosenblatt感知机

Rosenblatt感知机器

感知器在神经网络发展的历史上占据着特殊位置：它是第一个从算法上完整描述的神经网络。它的发明者Rosenblatt是一位心里学家，在20世纪60年代和70年代，感知器的启发，工程师、物理学家以及数学家们纷纷投身于神经网络各个不同方面的研究。值得一提的是，尽管在58年Rosenblatt关于感知器的论文就发表了，感知器在今天依然是有效的。

Rosenblatt感知器建立在一个非线性神经元上，即神经元的McCulloch-Pitts模型。如下图：

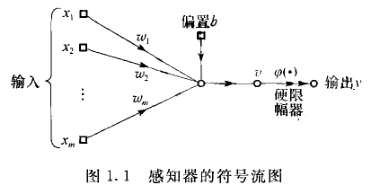
在上图中，感知器的突触权值即为w1,w2,...,wm。相应地，作用于感知器的输入记为x1,x2,...,xm。外部作用偏置记为b。从这个模型我们发现硬限幅器输入或神经元的诱导局部域是：

感知器的目的是把外部作用刺激X1,X2,...,Xm正确分为两类。分类规则是：如果感知器输出y是+1就将X1,X2,...,Xm表示的点分配给类1，如果感知器输出y=-1则分配给类2。

为了进一步观察模式分类器的行为，一般要再m维信号空间中画出决策区域图，这个空间是由m个输入变量X1,X2,...,Xm所张成的。在最简单的感知器中存在被一个超平面分开的两个决策域，此超平面定义为：

                   上面的实验和算法我会在下一篇单独用C++实现，整理上传。

总结：