Python算法-二叉树深度优先遍历

二叉树

组成：

1、根节点  BinaryTree：root

2、每一个节点，都有左子节点和右子节点（可以为空）  TreeNode：value、left、right

二叉树的遍历：

遍历二叉树：深度优先遍历、广度优先遍历。

广度：先遍历兄弟节点，再遍历子节点    

深度：先遍历子节点，再遍历兄弟节点

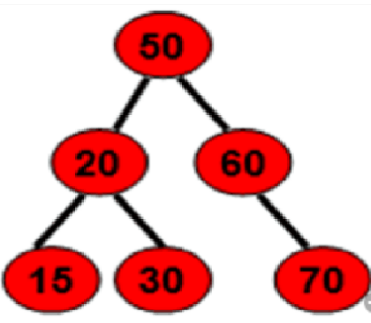
上图深度遍历结果：50/20/60/15/30/70

上图广度遍历结果：50/20/15/30/60/70

深度遍历又分为先序、中序、后序的遍历方式：

先序遍历：先根节点，再左子树，再右子树

上图先序遍历结果：50/20/ 15/ 30/ 60/ 70

中序遍历：先左子树，再根节点，再右子树

上图中序遍历结果：15/20/30/50/60/70

后序遍历：先左子树，再右子树，再根节点

上图后序遍历结果：15/30/20/70/60/50

代码实现：

# encoding=utf-8

class TreeNode(object): #定义二叉树类

def __init__(self,val,left=None,right=None):

self.val = val

self.left = left

self.right = right

class BinaryTree(object):

def __init__(self,root=None):

self.root = root

def preScan(self,retList, node): #先序遍历：先跟、再左、后右

if node != None:

retList.append(node.val)

self.preScan(retList, node.left)

self.preScan(retList, node.right)

return retList

def midScan(self, retList, node): #中序遍历：先左、再跟、后右

if node != None:

self.midScan(retList, node.left)

retList.append(node.val)

self.midScan(retList, node.right)

return retList

def postScan(self, retList, node): #后序遍历：先左、再右、后跟

if node != None:

self.postScan(retList, node.left)

self.postScan(retList, node.right)

retList.append(node.val)

return retList

if __name__ =='__main__':

root = TreeNode(50)

root.left = TreeNode(20,left=TreeNode(15),right=TreeNode(30,right=TreeNode(12)))

root.right = TreeNode(60,right=TreeNode(70))

bTree = BinaryTree(root)

retList = bTree.preScan([],bTree.root)

print retList

retList2 = bTree.midScan([],bTree.root)

print retList2

retList3 = bTree.postScan([],bTree.root)

print retList3