【集训队2017论文集】

一张无向图的Tutte矩阵为

其中xi,j为一个random的值。

Tutte矩阵的秩(一定为偶数)/2 就是这张图的最大匹配。

原理大概就是：

　　一个图有完美匹配，则det(A) <>0。

　　

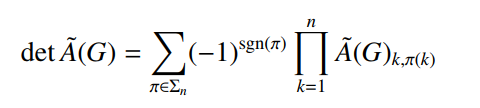
　　上面这个求det的式子中，每个偶环覆盖方案 都对应非零值，每个奇环覆盖方案 代进去都为0。

Tutte矩阵求一般图最大匹配的更多相关文章

  1. HDU 4687 Boke and Tsukkomi (一般图最大匹配)【带花树】

    <题目链接> 题目大意: 给你n个点和m条边,每条边代表两点具有匹配关系,问你有多少对匹配是冗余的. 解题分析: 所谓不冗余,自然就是这对匹配关系处于最大匹配中,即该匹配关系有意义.那怎样 ...

  2. [转]带花树,Edmonds's matching algorithm,一般图最大匹配

    看了两篇博客,觉得写得不错,便收藏之.. 首先是第一篇,转自某Final牛 带花树……其实这个算法很容易理解,但是实现起来非常奇葩(至少对我而言). 除了wiki和amber的程序我找到的资料看着都不 ...

  3. Ipad,IPhone（矩阵求递推项+欧拉定理）

    Ipad,IPhone Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total S ...

  4. 【Learning】带花树——一般图最大匹配

    一般图最大匹配--带花树 问题 ​ 给定一个图,求该图的最大匹配.即找到最多的边,使得每个点至多属于一条边. ​ 这个问题的退化版本就是二分图最大匹配. ​ 由于二分图中不存在奇环,偶环对最大匹配并无 ...

  5. 【题解】Uoj79一般图最大匹配

    带花树裸题,感觉带花树强强……不会的勿看此文,解释的可能不对,只是给自己看的!!!如题,带花树即为求一般图最大匹配算法(匈牙利与dinic为二分图最大匹配).推荐论文:2015年<浅谈图的匹配算 ...

  6. [一般图最大匹配]Bimatching

    10566 Bimatching 题意:一个男生必须跟两个女生匹配,求最大匹配 思路:一般的二分图匹配做不了,网络流也不会建图,这题采用的是一般图匹配 首先在原来二分图的基础上,将一个男生拆成两个点 ...

  7. 【模板】一般图最大匹配（带花树算法）/洛谷P6113

    题目链接 https://www.luogu.com.cn/problem/P6113 题目大意 给定一个 \(n\) 个点 \(m\) 条边的无向图,求该图的最大匹配. 题目解析 二分图最大匹配,一 ...

  8. UOJ79 一般图最大匹配

    题目描述 从前一个和谐的班级,所有人都是搞OI的.有 nn 个是男生,有 00 个是女生.男生编号分别为 1,-,n1,-,n. 现在老师想把他们分成若干个两人小组写动态仙人掌,一个人负责搬砖另一个人 ...

  9. [zt]矩阵求导公式

    今天推导公式,发现居然有对矩阵的求导,狂汗--完全不会.不过还好网上有人总结了.吼吼,赶紧搬过来收藏备份. 基本公式:Y = A * X --> DY/DX = A'Y = X * A --&g ...

随机推荐

  1. python 常见细节知识点

    1. a[::-1]翻转 设有一个元组或者列表 a = (1,2,3,4) b = [1,2,3,4] 则a[::-1]和b[::-1]的含义是将元组或列表的内容翻转 a[::-1] # 结果为(4, ...

  2. 理解Neural Style

    paperA Neural Algorithm of Artistic Style 在艺术领域,尤其是绘画,艺术家们通过创造不同的内容与风格,并相互交融影响来创立独立的视觉体验.如果给定两张图像,现在 ...

  3. angular md-toast 颜色

    How to show md-toast with background color https://codepen.io/neilkalman/pen/jWBqve <div ng-contr ...

  4. FFmpeg for ios架构：中级

    FFmpeg这部分想了非常久,也没找到比較好的解说方式.本来想像其他博客一样.对着代码一行行的分析.但后来感觉不太现实,FFmpeg应用在IOS上怎么说代码最少也有个5.6k行(包含音视频.业务逻辑) ...

  5. ZOJ 3626 Treasure Hunt I（树形dp）

    Treasure Hunt I Time Limit: 2 Seconds      Memory Limit: 65536 KB Akiba is a dangerous country since ...

  6. codefoeces B. Friends and Presents

    B. Friends and Presents time limit per test 1 second memory limit per test 256 megabytes input stand ...

  7. C语言-回溯例2

    组合问题 组合:从n个不同元素中取r个不重复的元素组成一个子集,而不考虑其元素的顺序,称为从n个中取r个的无重组合,例如OR = {1,2,3,4}, n = 4, r = 3则无重组合为: {1,2 ...

  8. [笔记] sed and awk

    / awk程序的典型示例是将数据转换成格式化的报表,当数据拥有某种结构时就能最好的体现awk的好处:可以使用awk脚本对数据的列重新排序,甚至可以将列变成行以及将行变成列:awk的功能将文本编辑的思想 ...

  9. centos7下MySQL的配置

    1. 下载mysql的repo源 wget http:.noarch.rpm 2. 安装mysql-community-release-el7-5.noarch.rpm包 rpm .noarch.rp ...

  10. 加载jsp页面报#{} is not allowed in template text

    问题是在引进jQueryUI时遇到 解决方法: 在page指令添加:             deferredSyntaxAllowedAsLiteral="true" 例如:&l ...