03-树1 树的同构（25 point(s)） 【Tree】

03-树1 树的同构（25 point(s)）

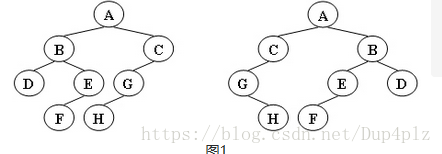
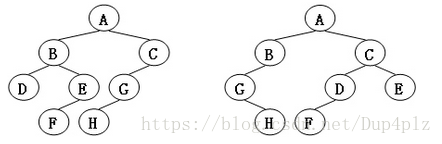
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

图1

图2

现给定两棵树，请你判断它们是否是同构的。

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8

A 1 2

B 3 4

C 5 -

D - -

E 6 -

G 7 -

F - -

H - -

8

G - 4

B 7 6

F - -

A 5 1

H - -

C 0 -

D - -

E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8

B 5 7

F - -

A 0 3

C 6 -

H - -

D - -

G 4 -

E 1 -

8

D 6 -

B 5 -

E - -

H - -

C 0 2

G - 3

F - -

A 1 4

输出样例2:

No

思路

因为 题目有一个限制条件 就是 每个结点存储的字母是不同的

所以 我们可以 以 字母 作为一个标记

意思就是

我们可以层序遍历 把每个结点的 字母 压入 字符串

最后比较 两个字符串 是否相同

就可以了

什么意思呢

就是 字母 是有一个 字典序的 然后 树的 同构的 定义 呢 就是 可以互换 左右儿子

那么 我们对于 每个 根节点 如果 同时存在 左右儿子 就将 字典序 小的 先 压入 队列 和 写入 字符串

这样 我们就 避免了 左右儿子的概念 如果 树 的同构的 那么最后得到的字符串 就是相同的

比如

左边 这棵树

得到的字符串 就是

ABCDEGFH

右边 这棵 树 得到的

ABCDEGFH

左边这棵树

ABCDEGFH

右边

ABCGDEHF

AC代码

#include <cstdio>
#include <cstring>
#include <ctype.h>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <map>
#include <stack>
#include <set>
#include <numeric>
#include <sstream>
#include <iomanip>
#include <limits>

#define CLR(a) memset(a, 0, sizeof(a))
#define pb push_back

using namespace std;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair <int, int> pii;
typedef pair <ll, ll> pll;
typedef pair<string, int> psi;
typedef pair<string, string> pss;

const double PI = 3.14159265358979323846264338327;
const double E = exp(1);
const double eps = 1e-30;

const int INF = 0x3f3f3f3f;
const int maxn = 1e5 + 5;
const int MOD = 1e9 + 7;

struct Node
{
    char c;
    int l, r;
}tree[2][10];

string s[2];

queue <int> q;

void bfs(int index)
{
    int len = q.size();
    for (int i = 0; i < len; i++)
    {
        int num = q.front();
        q.pop();
        s[index] += tree[index][num].c;
        if (tree[index][num].l != -1 && tree[index][num].r != -1)
        {
            if (tree[index][tree[index][num].l].c < tree[index][tree[index][num].r].c)
            {
                q.push(tree[index][num].l);
                q.push(tree[index][num].r);
            }
            else
            {
                q.push(tree[index][num].r);
                q.push(tree[index][num].l);
            }
        }
        else if (tree[index][num].l != -1)
            q.push(tree[index][num].l);
        else if (tree[index][num].r != -1)
            q.push(tree[index][num].r);

    }
    while (q.size())
        bfs(index);
}

int main()
{
    int n[2];
    map <int, int> m;
    char a, b, c;
    int root[2];
    for (int k = 0; k < 2; k++)
    {
        m.clear();
        scanf("%d", &n[k]);
        for (int i = 0; i < n[k]; i++)
        {
            scanf(" %c %c %c", &a, &b, &c);
            tree[k][i].c = a;
            if (isdigit(b))
            {
                tree[k][i].l = b - '0';
                m[b - '0'] = 1;
            }
            else
                tree[k][i].l = -1;
            if (isdigit(c))
            {
                tree[k][i].r = c - '0';
                m[c - '0'] = 1;
            }
            else
                tree[k][i].r = -1;
        }
        for (int i = 0; i < n[k]; i++)
        {
            if (m[i] == 0)
            {
                root[k] = i;
                break;
            }
        }
    }
    if (n[0] && n[1])
    {
        for (int i = 0; i < 2; i++)
        {
            s[i].clear();
            while (!q.empty())
                q.pop();
            q.push(root[i]);
            bfs(i);
        }
        if (s[0] == s[1])
            printf("Yes\n");
        else
            printf("No\n");
    }
    else
        printf("Yes\n");
}