POJ 1609 Tiling Up Blocks

Tiling Up Blocks

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4675		Accepted: 1824

Description

Michael The Kid receives an interesting game set from his grandparent as his birthday gift. Inside the game set box, there are n tiling blocks and each block has a form as follows: 

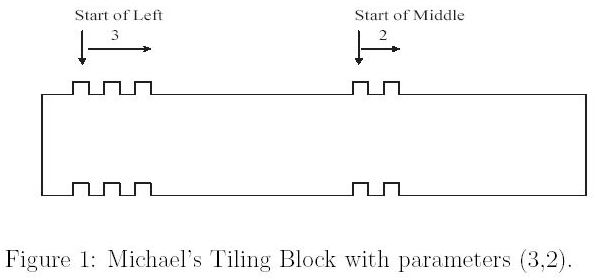
Each tiling block is associated with two parameters (l,m), meaning that the upper face of the block is packed with l protruding knobs on the left and m protruding knobs on the middle. Correspondingly, the bottom face of an (l,m)-block is carved with l caving dens on the left and m dens on the middle. 
It is easily seen that an (l,m)-block can be tiled upon another (l,m)-block. However,this is not the only way for us to tile up the blocks. Actually, an (l,m)-block can be tiled upon another (l',m')-block if and only if l >= l' and m >= m'. 
Now the puzzle that Michael wants to solve is to decide what is the tallest tiling blocks he can make out of the given n blocks within his game box. In other words, you are given a collection of n blocks B = {b1, b2, . . . , bn} and each block bi is associated with two parameters (li,mi). The objective of the problem is to decide the number of tallest tiling blocks made from B. 

Input

Several sets of tiling blocks. The inputs are just a list of integers.For each set of tiling blocks, the first integer n represents the number of blocks within the game box. Following n, there will be n lines specifying parameters of blocks in B; each line contains exactly two integers, representing left and middle parameters of the i-th block, namely, li and mi. In other words, a game box is just a collection of n blocks B = {b1, b2, . . . , bn} and each block bi is associated with two parameters (li,mi). 
Note that n can be as large as 10000 and li and mi are in the range from 1 to 100. 
An integer n = 0 (zero) signifies the end of input.

Output

For each set of tiling blocks B, output the number of the tallest tiling blocks can be made out of B. Output a single star '*' to signify the end of 
outputs.

Sample Input

3
3 2
1 1
2 3
5
4 2
2 4
3 3
1 1
5 5
0

Sample Output

2
3
*
题目大意：给定n个砖块的长和宽，只有当x2>=x1&&y2>=y1时 n2可以放在n1上 问最高能落多高。
解题方法：求最大不上升子序列，用动态规划。

#include <stdio.h>
#include <iostream>
#include <string.h>
using namespace std;

int main()
{
    int w[][];
    int dp[][];
    int n;
    while(scanf("%d", &n) != EOF)
    {
        if (n == )
        {
            printf("*\n");
            break;
        }
        int a, b;
        memset(w, , sizeof(w));
        memset(dp, , sizeof(dp));
        for (int i = ; i <= n; i++)
        {
            scanf("%d%d", &a, &b);
            w[a][b]++;
        }
        for (int i = ; i <= ; i++)
        {
            for (int j = ; j <= ; j++)
            {
                dp[i][j] = max(dp[i - ][j], dp[i][j - ]) + w[i][j];
            }
        }
        printf("%d\n", dp[][]);
    }
    return ;
}