POJ2513:Colored Sticks(字典树+欧拉路径+并查集）

http://poj.org/problem?id=2513

Description

You are given a bunch of wooden sticks. Each endpoint of each stick is colored with some color. Is it possible to align the sticks in a straight line such that the colors of the endpoints that touch are of the same color?

Input

Input is a sequence of lines, each line contains two words, separated by spaces, giving the colors of the endpoints of one stick. A word is a sequence of lowercase letters no longer than 10 characters. There is no more than 250000 sticks.

Output

If the sticks can be aligned in the desired way, output a single line saying Possible, otherwise output Impossible.

Sample Input

blue red
red violet
cyan blue
blue magenta
magenta cyan

Sample Output

Possible

Hint

Huge input,scanf is recommended.

大致题意：

给定一些木棒，木棒两端都涂上颜色，求是否能将木棒首尾相接，连成一条直线，要求不同木棒相接的一边必须是相同颜色的。

由图论知识可以知道，无向图存在欧拉路的充要条件为：

①     图是连通的；

②     所有节点的度为偶数，或者有且只有两个度为奇数的节点。

分析：欧拉路径问题，求是否有欧拉通路（欧拉回路的概念）

1.定理：无向图G有欧拉通路的充分必要条件是G为连通图，并且G仅有两个奇度结点或者无奇度结点。
（1）当G是仅有两个奇度结点的连通图时，G的欧拉通路必以此两个结点为端点。
（2）当G是无奇度结点的连通图时，G必有欧拉回路。

2.一个有向图D具有欧拉通路，当且仅当D是连通的，且除了两个顶点外，其余顶点的入度均等于出度，这两个特殊的顶点中，一个顶点的入度比出度大１，另一个顶点的入度比出度小１． 推论：一个有向图D是欧拉图（具有欧拉回路），当且仅当D是连通的，且所有顶点的出度等于入度。

3.trie树是一种存储名称的普遍方法。

解法：并查集判断是否连通，用trie存储每种颜色。看度是否符合要求。

题目解析：

如果不看题解根本不知道要用欧拉路径算法来做，这题之前一直没思路。。。这题有个坑就是你什么不输入输出也是Possible，其他就没什么注意的了。

欧拉路径就是一笔画问题。

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <stdlib.h>
#define N 500002
using namespace std;
typedef struct node
{
    int flag;
    struct node *next[];
}*Tree,Node;
char a[],b[];
int du[N+],bin[N+],num;
int findx(int x)
{
    int r=x;
    while(bin[r]!=r)
        r=bin[r];
    int j=x,k;
    while(j!=r)
    {
        k=bin[j];
        bin[j]=r;
        j=k;
    }
    return r;
}
void merge(int x,int y)
{
    int fx=findx(x);
    int fy=findx(y);
    if(fx!=fy)
        bin[fy]=fx;
}
void creat(Tree &T)
{
    T=(Tree )malloc(sizeof(Node));
    T->flag=;
    for(int i=; i<; i++)
        T->next[i]=NULL;
}
int inseart(Tree &T,char *s)
{
    int t,l,flag2=;;
    l=strlen(s);
    Tree p=T;
    for(int i=; i<l; i++)
    {
        t=s[i]-'a';
        if(p->next[t]==NULL)
        {
            creat(p->next[t]);
            flag2=;
        }
        p=p->next[t];
    }
    if(flag2==)
    {
        num++;
        p->flag=num;
        return p->flag;
    }
    return p->flag;
}
void delete1(Tree p)
{
    for(int i=; i<; i++)
    {
        if(p->next[i])
        {
            delete1(p->next[i]);
        }
    }
    free(p);
}
int main()
{
    Tree T;
    creat(T);
    for(int i=; i<=N; i++)
    {
        bin[i]=i;
        du[i]=;
    }
    num=;
    int sum=;
    while(scanf("%s%s",a,b)!=EOF)
    {
        int tx=inseart(T,a);
        du[tx]++;
        int ty=inseart(T,b);
        du[ty]++;
        merge(tx,ty);
    }
    for(int j=; j<=num; j++)
    {
        if(du[j]%)
            sum++;
        if(sum>)
        {
            printf("Impossible\n");
            delete1(T);
            return ;
        }
    }
    if(sum==) printf("Impossible\n");
    else
    {
        sum=;
        //int ss=findx(1);
        for(int i=; i<=num; i++)
        {
            if(i==bin[i])
                sum++;//这题有坑，如果什么不输入直接Crl+Z也是输出"Possible";

        }
        if(sum==||sum==) printf("Possible\n");
        else  printf("Impossible\n");
    }
    delete1(T);
    return ;
}

解题思路：

可以用图论中欧拉路的知识来解这道题，首先可以把木棒两端看成节点，把木棒看成边，这样相同的颜色就是同一个节点

问题便转化为：

给定一个图，是否存在“一笔画”经过涂中每一点，以及经过每一边一次。

这样就是求图中是否存在欧拉路Euler-Path。

回顾经典的“七桥问题”，相信很多同学马上就明白了什么是 欧拉路 了，这里不多作解释。

由图论知识可以知道，无向图存在欧拉路的充要条件为：

①     图是连通的；

②     所有节点的度为偶数，或者有且只有两个度为奇数的节点。

其中①图的连通性用程序判断比较麻烦，先放一下。

这里先说说②关于度数的判断方法：

Blue

Magenta

Violet

Cyan

Red

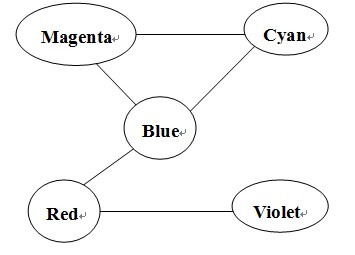
节点的度用颜色出现次数来统计，如样例中，蓝色blue出现三次（不管是出度还是入度），那么blue结点的度就为3，同样地，我们也可以通过输入得到其他全部结点的度，于是，我们有：

Blue=3

Red=2

Violet=1

Cyan=2

Magenta=2

用一个一维数组就能记录了，然后分别 模2，就能判断颜色结点的奇偶性

只要奇度数的结点数的个数 = 1 或 >=3 ，即使①图连通，欧拉路也必不存在

但是若 奇度数的结点数的个数 为0或 ==2，那么我们继续进行①图的连通性证明：

证明①图的连通性，使用并查集MergeSet是非常高效的方法。

知识考查点：

1、字典树；

2、欧拉路：其中又考察了判断是否为连通图；

3、并查集 及其优化方法（路径压缩）。

输出：

POSSIBLE：  奇度数结点个数==0 或 ==2  且  图连通

IMPOSSIBLE：奇度数结点个数==1 或 >=3  或  图不连通