关于博主skywang123456文章——二叉堆(三)之 Java的实现的质疑

博客园博主skywang123456(以下简称s博主)是一个大牛级的人物，相信很多程序员都拜读过他的博客，我也不例外，并且受益匪浅。但是对于文章二叉堆(三)之 Java的实现我有一些疑惑，写在这里，供有缘人参考。对于而二叉堆的插入，是一个较为简单的方法，这里没有什么问题。但是而二叉堆的删除确是一个稍微复杂一点的操作，事实上，我第一次看这篇博文的时候就感觉有些恍惚不清。一般来说，而二叉堆的删除分为删除堆顶和查找型删除。堆顶删除可以由查找型删除实现，故名思意，直接删除堆顶的数据即可，在二叉堆的实际应用中被广泛使用。而查找型删除首先要查到给定参数的位置，然后删除该元素。而我要指出的问题是博主s使用删除堆顶的代码来代替了查找型删除的代码，而这两个我会举例来说明是不同的。

先来看博主s的删除代码

public int remove(T data) {
    // 如果"堆"已空，则返回-1
    if(mHeap.isEmpty() == true)
        return -1;

    // 获取data在数组中的索引
    int index = mHeap.indexOf(data);
    if (index==-1)
        return -1;

    int size = mHeap.size();
    mHeap.set(index, mHeap.get(size-1));// 用最后元素填补
    mHeap.remove(size - 1);                // 删除最后的元素

    if (mHeap.size() > 1)
        filterdown(index, mHeap.size()-1);    // 从index号位置开始自上向下调整为最小堆

    return 0;
}

protected void filterdown(int start, int end) {
    int c = start;          // 当前(current)节点的位置
    int l = 2*c + 1;     // 左(left)孩子的位置
    T tmp = mHeap.get(c);    // 当前(current)节点的大小

    while(l <= end) {
        int cmp = mHeap.get(l).compareTo(mHeap.get(l+1));
        // "l"是左孩子，"l+1"是右孩子
        if(l < end && cmp<0)
            l++;        // 左右两孩子中选择较大者，即mHeap[l+1]
        cmp = tmp.compareTo(mHeap.get(l));
        if(cmp >= 0)
            break;        //调整结束
        else {
            mHeap.set(c, mHeap.get(l));
            c = l;
            l = 2*l + 1;
        }
    }
    mHeap.set(c, tmp);
}

不难理解，将查找到的节点使用堆尾数据填充，之后删除堆尾数据，接着从该节点自上往下调整为最小堆。(目测笔误，应该是最大堆)这是典型的删除堆顶的代码。

博主s在文中给了两个删除的例子。第一个是删除堆顶的元素，因为没有根节点，所以当然适合这个代码。

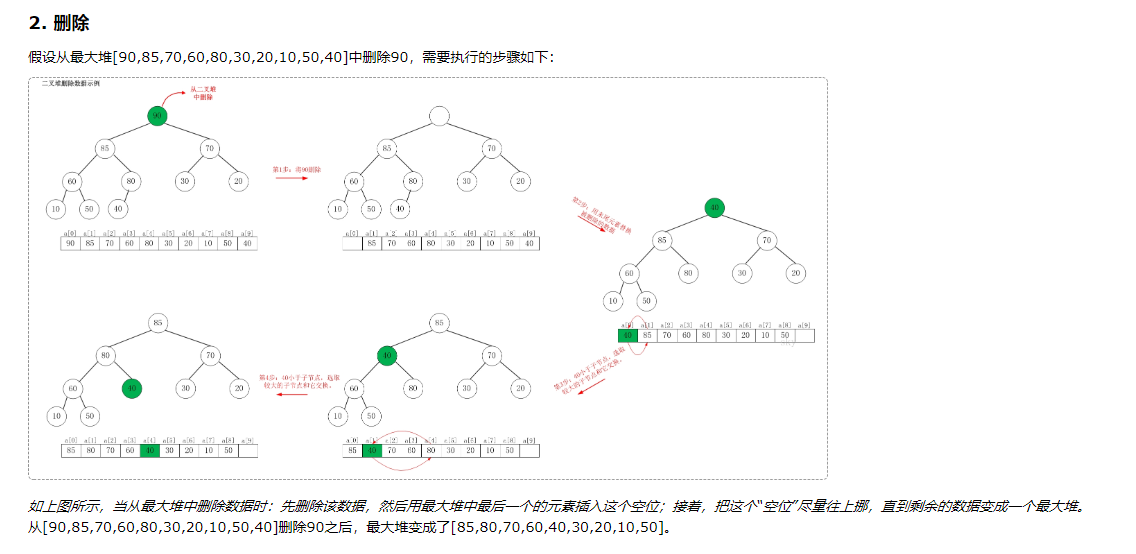
而第二个例子不是删除根节点的数据，但是为什么也可以？这是一个巧合，恰好是符合某些特定的条件。

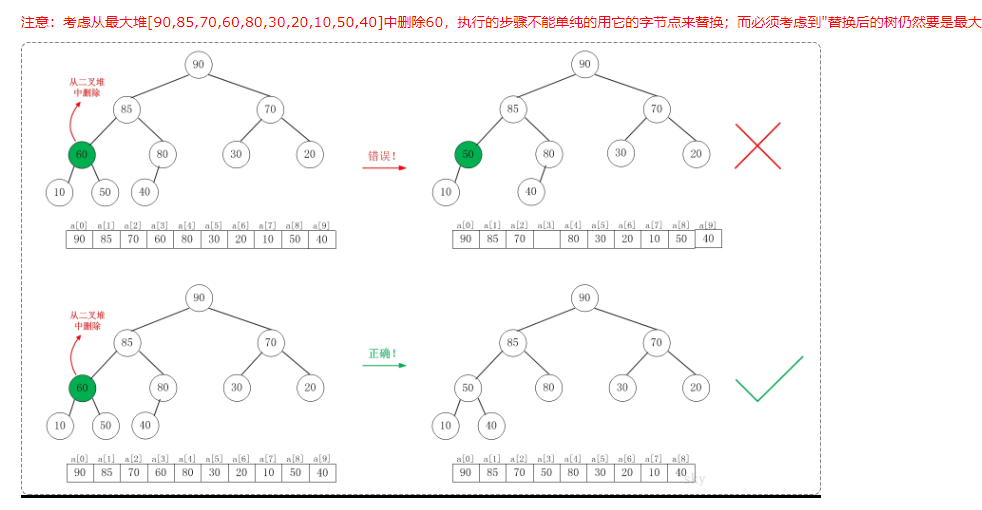
如图所示，删除节点60，补充40，40小于其子节点50，然后交换。其实有一种情况，即堆尾数据补充之后会大于原先的父节点，我们来看下图这个堆。

                  

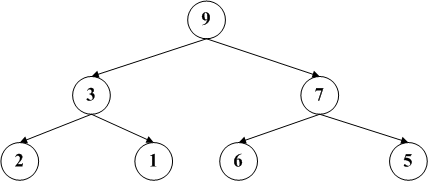
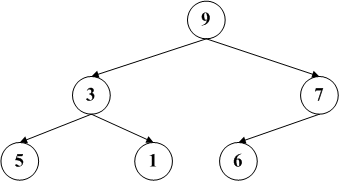
如果我们删除节点2，按照博主s的步骤，将5补充到原有节点2的位置，然后删除原有节点5，这样就变成右图。之后由于没有子节点，因此结束删除操作。可是右边是一个最大堆吗？显然不是！

所以查找型删除应该添加一个步骤，即先判断是否大于父节点(对于最大堆来说)，如果大于父节点，则进行向上交换，直到符合最大堆的条件。查找型删除可以参考我这一篇文章二叉堆的介绍和Java实现 。当然我的代码没有过多测试，可能也有没有考虑到的地方，欢迎大家直接勘误。

以上，便是我看完这篇博文的一些质疑和思考，所说的不一定都对。当然，即使博主s真的有失误，也不影响我这么长时间看他博文所获得的进步。