Linear Algebra lecture8 note

Compute solution of AX=b (X=Xp+Xn)

rank r

r=m solutions exist

r=n solutions unique

 

---

example:

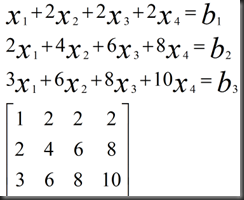
若想方程有解，b1,b2,b3需要满足什么条件？ 观察矩阵可知，第三行是前两行的和，所以b1+b2=b3

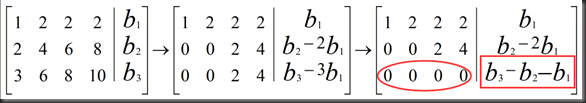
Solvability Condition on b:

Ax=b is solvable when b is in C (A)

If a combination of Rows of A gives zero row, then the same combination of entries of b must give 0

假设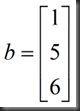，则上述矩阵变为：

To find complete solution to AX=b:

1.Xp (particular): set all free variables to zero, solve AX=b for pivot variable

此例中，X2=0，X4=0

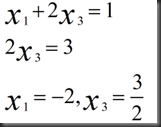
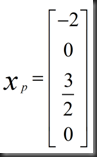
2.Xn(nullspace) 上一节已经解出

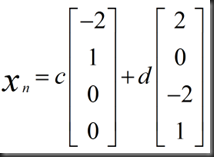
3.X(complete)=Xp+Xn

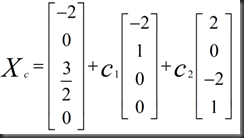
以上操作可解释为：

 

---

m by n matrix A of rank r(r<=m,r<=n)

Full column of rank(r=n):

所有列均有主元; no free variables;  N(A)=zero vector; solution to AX=b is X=Xp which means if solution exists then the solution is unique(0 or 1 solution)

这种情况实际就是，除zero组合之外，列之间的线性组合无法产生零列

Full row of rank(r=m):

所有行均有主元; no zero rows; can solve AX=b for every b; left with n-r(n-m) free variables

Full rank(r=m=n):

N(A)=zero vector; R(行最简形）=I（单位矩阵）

 

summary：

矩阵的秩决定了方程组解的数目