“计数质数”问题的常规思路和Sieve of Eratosthenes算法分析

题目描述

题目来源于 LeetCode 204.计数质数，简单来讲就是求“不超过整数 n 的所有素数个数”。

常规思路

一般来讲，我们会先写一个判断 a 是否为素数的 isPrim(int a) 函数：

bool isPrim(int a){
	for (int i = 2; i < a; i++)
		if (a % i == 0)//存在其它整数因子
			return false;
	return true;
}

然后我们会写一个 countIsPrim(int n) 来计算不超过 n 的所有素数个数：

int countPrimes(int n) {
    int ans = 0;
    for (int i = 2; i < n; i++)
        if (isPrim(i))	ans++;
    return ans;
}

显然这两个嵌套的 for 循环时间复杂度是 \(O(n^2)\) ，但是这样写有两个主要的问题：

1. isPrim() 函数的计算冗余。首先，举个例子引入一下因子的对称性：

   12 = 2 × 6
   12 = 3 × 4
   12 = sqrt(12) × sqrt(12)
   12 = 4 × 3
   12 = 6 × 2
   

   所以当循环判断一个数 \(a\) 是否有除了 1 和它本身之外其余的因子时，我们只需要将循环变量终止在 \(\sqrt a\) 的位置，而非 [2, a) 的所有数。

2. countPrimes(int n)函数的计算冗余。例如，一旦我们判断2为质数那么所有2的倍数一定都是质数，如果我们知道3是质数，那么所有3的倍数也一定都是质数。所以如果我们将 [2, n) 的数都进行一次 isPrim() ，那么将带来巨大的时间浪费。

我们在这里，先将第一个问题解决，即优化 isPrim() 函数：

bool isPrim(int n){
    //根据因子对称性
	for (int i = 2; i * i <= n; i++){
		if (n % i == 0)//存在其它整数因子
            return false;
	}
    return true;
}

采用 Sieve of Eratosthenes 算法高效实现

这个算法的中文叫作“埃拉托斯特尼筛法”，听起来很复杂，但是并不难理解，本质上就是把常规思路反过来，如下面动图所示：

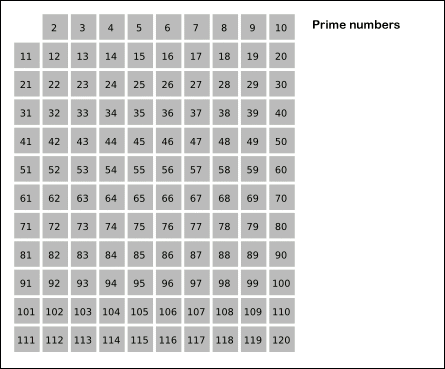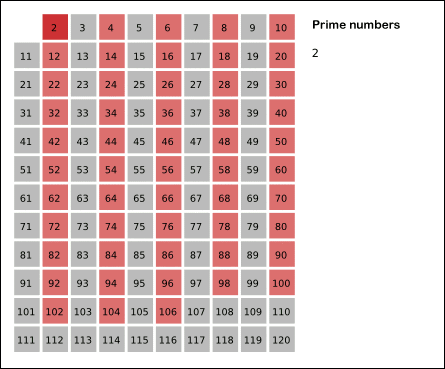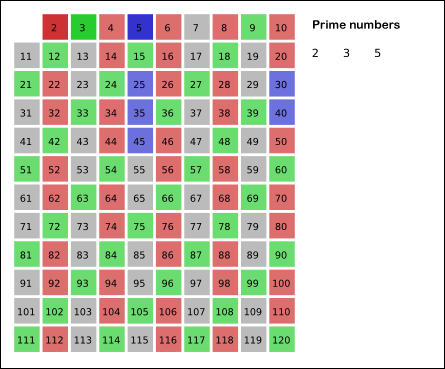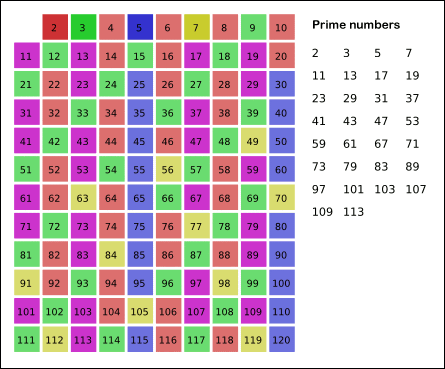
下面我们逐渐引出该算法的全貌：

常规思路就是将区间为 [2, n) 的数都遍历一遍，在过程中累加素数的个数。上述问题二已经说明了其低效性，根据“如果 i 是质数，那么所有 i 的倍数都不是质数”，我们做出优化：

int countPrimes(int n) {
	vector<int> IsPrim(n + 1, true);
	for (int i = 2; i < n; i++){
		if (isPrim[i]){
            //如果i是质数，那么所有i的倍数都不是质数
			for (int j = 2 * i; j < n; j += i){
				IsPrim[j] = false;
			}
		}
	}
	//遍历一遍计算结果
	int ans = 0;
	for (int i = 2; i < n; i++){
		if (IsPrim[i])	ans++;
	}
    return ans;
}

这段代码展现了该算法的整体思路，但是还有两个细节可以优化：

1. 由于因子的对称性，我们可以将外层 for 循环改为：for (int i = 2; i * i < n; i++) 。
2. 将内层循环改为：for (int j = i * i; j < n; j += i) 。举个例子， n = 25 ，当 i = 4 时算法会标记 4 × 2 = 8，4 × 3 = 12 等等数字，但是这两个数字已经被 i = 2 和 i = 3 的 2 × 4 和 3 × 4 标记了。所以我们可以从平方项开始遍历。

到这里，Sieve of Eratosthenes 算法就已经实现了，下面给出完整的代码：

int countPrimes(int n) {
    vector<int> prims(n + 1, 1);
    for (int i = 2; i * i < n; i++){
        if (isPrim[i]){
            //如果i是质数，那么所有i的倍数都不是质数
            for (int j = i * i; j < n; j += i){
                prims[j] = 0;
            }
        }
    }
    //遍历一遍计算结果
    int ans = 0;
    for (int i = 2; i < n; i++){
        if(prims[i])	ans++;
    }
	return ans;
}

Sieve of Eratosthenes 算法的证明

该算法的时间复杂度为 \(O(nloglogn)\) ，下面给出三个公式和证明：

\(Prerequisite\).

调和级数（Harmonic series）是一个发散的无穷级数，当 \(n\) 趋近于无穷大时，有一个近似公式：

\[1+\frac{1}{2}+\frac{1}{3}+\cdot\cdot\cdot\frac{1}{n} = \sum_{i=1}^{n}\frac{1}{i} = ln(n) + \gamma
\]

其中 \(\gamma\) 为欧拉常数，\(\gamma \approx 0.57721\)

泰勒级数（Taylor series）是1715年英国数学家布鲁克·泰勒提出的，在零点的导数求得的泰勒级数又叫麦克劳林级数，一个常用的泰勒级数如下：

\[ln\frac{1}{1-x} = \sum^{\infty}_{n=1}\frac{x^n}{n} = x + \frac{x^2}{2} + \frac{x^3}{3} + \cdot\cdot\cdot+\frac{x^n}{n}
\]

对任意 \(x \in [-1,1)\) 都成立。

欧拉乘积公式（Euler product）是著名的瑞士数学家欧拉于1737年在俄罗斯的圣彼得堡科学院发表的重要公式，为数学家研究素数的分布奠定了基础，即：

\[\sum_{n}^{}\frac{1}{n^{s}} = \prod_{p}^{1}\frac{1}{1-p^{-s}}
\]

其中 \(n\) 是自然数，\(p\) 为素数。

---

\(Prove.\)

该算法的运行时间可以看作筛除的次数之和：

\[\frac{n}{2}+\frac{n}{3}+\frac{n}{5}+ \cdot \cdot \cdot +\frac{n}{p} = n \cdot (\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+ \cdot \cdot \cdot +\frac{1}{p}) = n \sum_{p}\frac{1}{p}
\]

显然我们需要想办法处理后面的质数倒数和。我们拿出欧拉乘机公式，将所有的 \(s\) 用1来代替：

\[\sum_{n}^{}\frac{1}{n} = \prod_{p}^{1}\frac{1}{1-p^{-1}}
\]

两侧同时取对数：

\[ln(\sum_{n}^{}\frac{1}{n}) = \sum_{p}^{}ln\frac{1}{1-p^{-1}}
\]

由于 \(-1< p^{-1} < 1\) ，所以对上面右侧求和的每一项进行泰勒展开得到：

\[ln\frac{1}{1-p^{-1}} = \sum^{\infty}_{n=1}\frac{1}{np^{n}} = \frac{1}{p} + \frac{1}{2p^2} + \frac{1}{3p^3} + \cdot\cdot\cdot + \frac{1}{np^n}
\]

故得到：

\[
\begin{equation}
\begin{split}
ln(\sum_{n}^{}\frac{1}{n}) &= \sum_{p}^{}\frac{1}{p} + \sum_{p}^{}\frac{1}{p^2}(\frac{1}{2} + \frac{1}{3p} + \frac{1}{4p^2}+\cdot\cdot\cdot)\\
&< \sum_{p}^{}\frac{1}{p} + \sum_p\frac{1}{p^2}(1+\frac{1}{p}+\frac{1}{p^2}+\cdot\cdot\cdot)\\
&= \sum_{p}^{}\frac{1}{p}+\sum_p\frac{1}{p(p-1)}\\
&= \sum_p\frac{1}{p} + C
\end{split}
\end{equation}
\]

上式左侧带入调和级数，当 \(n\) 趋向于无穷时得到：

\[\sum_{p}^{}\frac{1}{p} = ln(ln(n))
\]

到这里就成功处理掉了质数倒数和，所以时间复杂度为 \(O(nloglogn)\) 。

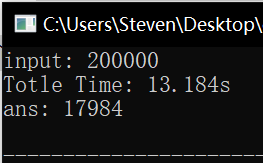
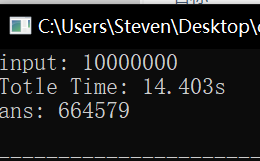
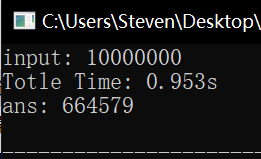
耗时比较

未改进版 \(isPrim()\) 、改进版 \(isPrim()\) 、高效算法三者耗时对比如下，可以看出来差距还是很大的：

参考资料

1. 埃拉托斯特尼筛法

2. 这个大概是唯一一个证明了时间复杂度的题解了！~

3. 如何高效寻找素数

4. Divergence of the sum of the reciprocals of the primes

5. 素数的倒数之和