矩阵十题【五】 VOJ1049 HDU 2371 Decode the Strings

题目链接：https://vijos.org/p/1049

题目大意：顺次给出m个置换，重复使用这m个置换对初始序列进行操作。问k次置换后的序列。m<=10, k<2^31。

首先将这m个置换“合并”起来（算出这m个置换的乘积），然后接下来我们须要运行这个置换k/m次（取整。若有余数则剩下几步模拟就可以）。

注意随意一个置换都能够表示成矩阵的形式。比如。将1 2 3 4置换为3 1 2 4，相当于以下的矩阵乘法：

置换k/m次就相当于在前面乘以k/m个这种矩阵。

我们能够二分计算出该矩阵的k/m次方，再乘以初始序列就可以。做出来了别忙着高兴。得意之时就是你灭亡之日。别忘了最后可能还有几个置换须要模拟。

注意：这m个置换相应的矩阵相乘的时候必须左乘

代码例如以下：

///https://vijos.org/p/1049
#include<iostream>
#include<stdio.h>
#include<cstring>
using namespace std;
const int MAX = 105;

struct Matrix
{
    int v[MAX][MAX];
};

int n,m,k;  //分别代表的是每一个置换的长度
            //置换的一组的个数
            //以及一共置换的操作

Matrix mtAdd(Matrix A, Matrix B)        // 求矩阵 A + B
{
    int i, j;
    Matrix C;
    for(i = 0; i < n; i ++)
        for(j = 0; j < n; j ++)
            C.v[i][j]=(A.v[i][j]+B.v[i][j]);
    return C;
}

Matrix mtMul(Matrix A, Matrix B)        // 求矩阵 A * B
{
    int i, j, k;
    Matrix C;
    for(i = 0; i < n; i ++)
        for(j = 0; j < n; j ++)
        {
            C.v[i][j] = 0;
            for(k = 0; k < n; k ++)
                C.v[i][j] = (A.v[i][k] * B.v[k][j] + C.v[i][j]);
        }
    return C;
}

Matrix mtPow(Matrix A, int k)           // 求矩阵 A ^ k
{
    if(k == 0)
    {
        memset(A.v, 0, sizeof(A.v));
        for(int i = 0; i < n; i ++)
            A.v[i][i] = 1;
        return A;
    }
    if(k == 1) return A;
    Matrix C = mtPow(A, k / 2);
    if(k % 2 == 0)
        return mtMul(C, C);
    else
        return mtMul(mtMul(C, C), A);
}

void out(Matrix A)
{
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        cout<<A.v[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
}

int  main ()
{
    int mp[15][105];
    scanf("%d%d%d",&n,&m,&k);
    int shang=k/m;
    int yushu=k%m;
    Matrix ans;
    Matrix rig;
    Matrix B;
    Matrix tem;

    for(int i=0;i<n;i++) rig.v[0][i]=i+1;    //out(rig);

    memset(ans.v,0,sizeof(ans.v));
    for(int i=0;i<n;i++) ans.v[i][i]=1;

    for(int i=0;i<m;i++)
    {
        memset(B.v,0,sizeof(B.v));
        for(int j=0;j<n;j++)
        scanf("%d",&mp[i][j]),B.v[mp[i][j]-1][j]=1;
        //out(B);
        ans=mtMul(ans,B);
        if(i==yushu-1) tem=ans;
    }
    //out(ans);
    //out(tem);
    ans=mtPow(ans,shang);
    ans=mtMul(ans,tem);
    //out(ans);
    ans=mtMul(rig,ans);
    for(int i=0;i<n;i++) cout<<ans.v[0][i]<<" ";
    return 0;
}

hdu 2371 题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2371

题目大意：给出n 和m，给出n个数，代表一个置换，接着一个字符串s，s经过m次置换后变成还有一个字符串，

如今给出经过m次置换后的字符串，输出原始字符串s

比方：5 3

2 3 1 5 4

hello

需经过3次置换，则"hello" -> "elhol" -> "lhelo" -> "helol"

思路：将置换规则取反（将p[i]位置上的数num[i]变成p[num[i]]上的数。比如，num:  2 3 1 5 4  变成  num:  3 1 2 5 4

p: 1 2 3 4 5               p:  1 2 3 4 5  ）

然后将m次置换合并起来，即算出这m个置换的乘积（即origin^m)。然后乘以初始序列[1 2 3 4 ....n],然后输出相应位置的字符就可以。

注意随意一个置换都能够表示成矩阵的形式。比如，将1 2 3 4置换为3 1 2 4，相当于以下的矩阵乘法：

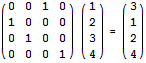
m次置换就相当于前面乘以m个这种矩阵。用矩阵高速幂就可以。

由于没有看清楚题意。第二组例子一直过不了，好心酸.......

///https://vijos.org/p/1049
#include<iostream>
#include<stdio.h>
#include<cstring>
using namespace std;
const int MAX = 105;

struct Matrix
{
    int v[MAX][MAX];
};

int n,p;

Matrix mtAdd(Matrix A, Matrix B)        // 求矩阵 A + B
{
    int i, j;
    Matrix C;
    for(i = 0; i < n; i ++)
        for(j = 0; j < n; j ++)
            C.v[i][j]=(A.v[i][j]+B.v[i][j]);
    return C;
}

Matrix mtMul(Matrix A, Matrix B)        // 求矩阵 A * B
{
    int i, j, k;
    Matrix C;
    for(i = 0; i < n; i ++)
        for(j = 0; j < n; j ++)
        {
            C.v[i][j] = 0;
            for(k = 0; k < n; k ++)
                C.v[i][j] = (A.v[i][k] * B.v[k][j] + C.v[i][j]);
        }
    return C;
}

 Matrix mtPow(Matrix origin,int k)  //矩阵高速幂
 {
     int i;
     Matrix res;
     memset(res.v,0,sizeof(res.v));
     for(i=1;i<=n;i++)
         res.v[i][i]=1;
     while(k)
     {
         if(k&1)
             res=mtMul(res,origin);
         origin=mtMul(origin,origin);
         k>>=1;
     }
     return res;
 }

void out(Matrix A)
{
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        cout<<A.v[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
}

int  main ()
{
    while(~scanf("%d%d",&n,&p))
    {
        if(n==0&&p==0) break;
    int num[90];
    Matrix A;
    Matrix B;
    memset(B.v,0,sizeof(B.v));
    for(int i=0;i<n;i++) B.v[0][i]=i;
    memset(A.v,0,sizeof(A.v));

    for(int i=0;i<n;i++) scanf("%d",&num[i]),A.v[i][num[i]-1]=1;
    //out(A);
    getchar();
    char c[90];
    for(int i=0;i<n;i++) scanf("%c",&c[i]);

    Matrix ans;
    ans=mtPow(A,p);
    //out(ans);
    ans=mtMul(B,ans);
    for(int i=0;i<n;i++) cout<<c[ans.v[0][i]];
    cout<<endl;
    }
}