BZOJ 2440 莫比乌斯函数+容斥+二分

2440: [中山市选2011]完全平方数

Time Limit: 10 Sec  Memory Limit: 128 MB
Submit: 5473  Solved: 2679
[Submit][Status][Discuss]

Description

小 X 自幼就很喜欢数。但奇怪的是，他十分讨厌完全平方数。他觉得这些
数看起来很令人难受。由此，他也讨厌所有是完全平方数的正整数倍的数。然而
这丝毫不影响他对其他数的热爱。 
这天是小X的生日，小 W 想送一个数给他作为生日礼物。当然他不能送一
个小X讨厌的数。他列出了所有小X不讨厌的数，然后选取了第 K个数送给了
小X。小X很开心地收下了。 
然而现在小 W 却记不起送给小X的是哪个数了。你能帮他一下吗？

Input

包含多组测试数据。文件第一行有一个整数 T，表示测试
数据的组数。 
第2 至第T+1 行每行有一个整数Ki，描述一组数据，含义如题目中所描述。

Output

含T 行，分别对每组数据作出回答。第 i 行输出相应的
第Ki 个不是完全平方数的正整数倍的数。

Sample Input

4
1
13
100
1234567

Sample Output

1
19
163
2030745

HINT

对于 100%的数据有 1 ≤ Ki ≤ 10^9,   T ≤ 50

莫比乌斯函数、反演

https://www.cnblogs.com/AOQNRMGYXLMV/p/4065628.html

 题意 输出第ki大的无平方因子数

 解析 无平方因子数可以线性筛，但是筛出来1e9个肯定超时。 我们对答案进行二分mid，转化成求 1~mid 有多少个无平方因子数

根据容斥原理我们可以求出答案，减去(一个素数的平方  的倍数 ）+ 加上（两个素数的乘积 的平方 的倍数）-....+...

比如说100以内 首先删掉  2的平方(4)的倍数 ，3的平方(9)的倍数......   会发现同时为4和9的倍数(e.g. 36 )被删了两遍  所以再把2*3(6)的平方36的倍数加回来.

要是枚举组合情况太麻烦了 我们发现一个数 a 的容斥系数就是u(a) (莫比乌斯函数) 所以答案就是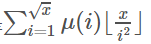   

复杂度O(T*log(n)*sqrt(n))

AC代码

 #include <bits/stdc++.h>
 #define pb push_back
 #define mp make_pair
 #define fi first
 #define se second
 #define all(a) (a).begin(), (a).end()
 #define fillchar(a, x) memset(a, x, sizeof(a))
 #define huan printf("\n");
 #define debug(a,b) cout<<a<<" "<<b<<" ";
 using namespace std;
 const int maxn=1e5+,inf=0x3f3f3f3f;
 typedef long long ll;
 typedef pair<int,int> pii;
 int check[maxn],prime[maxn],mu[maxn];
 void Mobius(int N)//莫比乌斯函数线性筛
 {
     int pos=;mu[]=;
     for (int i =  ; i <= N ; i++)
     {
         if (!check[i])
             prime[pos++] = i,mu[i]=-;
         for (int j =  ; j < pos && i*prime[j] <= N ; j++)
         {
             check[i*prime[j]] = ;
             if (i % prime[j] == )
             {
                 mu[i*prime[j]]=;
                 break;
             }
             mu[i*prime[j]]=-mu[i];
         }
     }
 }int solve(int n)
 {
     int temp=sqrt(n),ans=;
     for(int i=;i<=temp;i++)
         ans+=mu[i]*n/(i*i);
     return ans;
 }
 int main()
 {
     int t,n;
     Mobius();
     scanf("%d",&t);
     while(t--)
     {
         scanf("%d",&n);
         int l=,r=2e9,ans;
         while(l<=r)
         {
             int mid=l+(r-l)/;
             if(solve(mid)>=n) //不能直接等于n 二分的数不一定是无平方因子数
                 r=mid-;
             else
                 l=mid+;
         }
         printf("%d\n",r+);
     }
 }