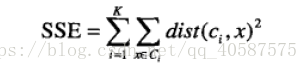数据挖掘-聚类分析（Python实现K-Means算法）

概念：

聚类分析（cluster analysis ）：是一组将研究对象分为相对同质的群组（clusters）的统计分析技术。聚类分析也叫分类分析，或者数值分类。聚类的输入是一组未被标记的样本，聚类根据数据自身的距离或者相似度将其划分成若干个组，划分的原则是组内距离最小化而组间（外部）距离最大化。聚类和分类的不同在于：聚类所要求划分的类是未知的。

聚类度量的方法：分距离和相似度来度量。

​

​

聚类研究分析的方法：

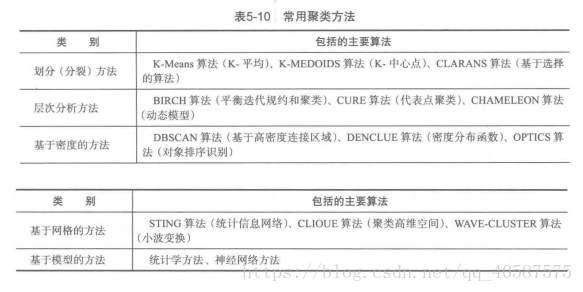
1.层次的方法（hierarchical  method）

2.划分方法（partitioning method）

3.基于密度的方法（density-based method）DBSCAN

4.基于网格的方法（grid-based method）

5.基于模型的方法（model-based method）

​

•K-Means 算法：

•受离群点的影响较大，由于其迭代每次的中心点到全部样本点的距离和的平均值。

优点：

• 原理简单
• 速度快
• 对大数据集有比较好的伸缩性

缺点：

• 需要指定聚类 数量K
• 对异常值敏感
• 对初始值敏感

•以欧式距离来衡量距离大小，使用误差平方和（Sum of the Squared Error,SSE）作为聚类的目标函数：

​

k表示k个聚类中心，ci表示第几个中心，dist表示的是欧几里得距离

​

•算法步骤；

•创建k个点作为初始的质心点（随机选择）

•当任意一个点的簇分配结果发生改变时

•       对数据集中的每一个数据点

•              对每一个质心

•                     计算质心与数据点的距离

•              将数据点分配到距离最近的簇

•       对每一个簇，计算簇中所有点的均值，并将均值作为质心

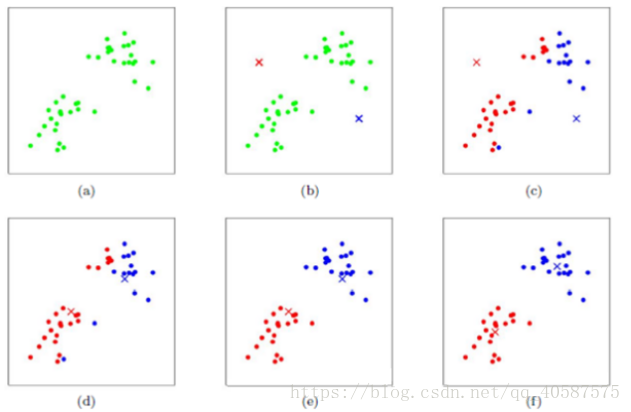
•算法图示：

​

Python代码实现K-Means算法：

有关于 .A 的用法：（flatten()函数可以是多维数组变换成一维数组， .A 则使得matrix 形式转化成 array 形式）

>>> import numpy as np
>>> demo_a2 = np.mat([[1,3],[2,4],[3,5]])
>>> demo_a2
matrix([[1, 3],
        [2, 4],
        [3, 5]])
>>> demo_a2.flatten()
matrix([[1, 3, 2, 4, 3, 5]])
>>> demo_a2.flatten().A
array([[1, 3, 2, 4, 3, 5]])
>>> demo_a2.flatten().A[0]
array([1, 3, 2, 4, 3, 5])

#定义一个欧式距离的函数 :

#coding=gbk
'''
Created on 2018年7月17日

@author: Administrator
'''
# k-means 算法python实现

import numpy as np

def distEclud(vecA, vecB):  #定义一个欧式距离的函数
    return np.sqrt(np.sum(np.power(vecA - vecB, 2)))

print('----test_distEclud-----')
vecA, vecB = np.array([1,1]), np.array([2,1])
distance = distEclud(vecA, vecB)
print(distance) # 1.0 计算两点之间的距离

随机设置k个中心点：

def randCent(dataSet, k):  #第一个中心点初始化
    n = np.shape(dataSet)[1]
    centroids = np.mat(np.zeros([k, n]))  #创建 k 行 n列的全为0 的矩阵
    for j in range(n):
        minj = np.min(dataSet[:,j]) #获得第j 列的最小值
        rangej = float(np.max(dataSet[:,j]) - minj)     #得到最大值与最小值之间的范围
        #获得输出为 K 行 1 列的数据，并且使其在数据集范围内
        centroids[:,j] = np.mat(minj + rangej * np.random.rand(k, 1))
    return centroids

print('----test_randCent-----')
dataSet1 = np.array([[1,2],[3,6],[8,10],[12,23],[10,11],[13,18]])
print(dataSet1[1,:])
r = randCent(dataSet1, 2)
print(r)
# [[ 8.83544015 16.75467081]
#  [ 2.85688493  4.4799291 ]]

np.random.seed(666) #定义一个随机种子
rand_num = np.random.rand(3,1)  #输出为3行1 列,随机数在 0 到 1 之间
print(rand_num)
# [[0.70043712]
#  [0.84418664]
#  [0.67651434]]
test = np.mat(np.zeros([3,2]))  #此处的 zeros 函数内的矩阵形式需要加中括号 []
print(test)
# [[0. 0.]    #打印出 3行 2列的矩阵
#  [0. 0.]
#  [0. 0.]] 

定义KMeans函数：

#参数： dataSet 样本点， K 簇的个数
#disMeans 距离， 默认使用欧式距离， createCent 初始中心点的选取
def KMeans(dataSet, k, distMeans= distEclud, createCent= randCent):
    m = np.shape(dataSet)[0]    #得到行数，即为样本数
    clusterAssement = np.mat(np.zeros([m,2]))   #创建 m 行 2 列的矩阵
    centroids = createCent(dataSet, k)      #初始化 k 个中心点
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):
            minDist = np.inf   #初始设置值为无穷大
            minIndex = -1
            for j in range(k):
                #  j循环，先计算 k个中心点到1 个样本的距离，在进行i循环，计算得到k个中心点到全部样本点的距离
                distJ = distMeans(centroids[j,:], dataSet[i,:])
                if distJ <  minDist:
                    minDist = distJ #更新 最小的距离
                    minIndex = j
            if clusterAssement[i,0] != minIndex:    #如果中心点不变化的时候， 则终止循环
                clusterChanged = True
            clusterAssement[i,:] = minIndex, minDist**2 #将 index，k值中心点 和  最小距离存入到数组中
        print(centroids)

        #更换中心点的位置
        for cent in range(k):
            ptsInClust = dataSet[np.nonzero(clusterAssement[:,0].A == cent)[0]] #分别找到属于k类的数据
            centroids[cent,:] = np.mean(ptsInClust, axis = 0)   #得到更新后的中心点
    return centroids, clusterAssement 

print('------test-----')
demo_a = np.array([[1,0],[0,2],[0,0]])
non_a = np.nonzero(demo_a)
print(demo_a)
# [[1 0]
#  [0 2]
#  [0 0]]
print(non_a)
# 输出的第一行为 行数， 第二行为列数,意思为   1行1列的数 和2行2列的数 是非0数
# (array([0, 1], dtype=int64), array([0, 1], dtype=int64))

demo_a1 = np.array([1,2,0,0,1]) #当只有一行时
non_a1 = np.nonzero(demo_a1)
print(non_a1)   # (array([0, 1, 4], dtype=int64),)  

a1 = np.inf > 100000
print(a1)       #  True   inf 是无穷大

print('---------- test KMeans ---------')
dataSet = np.mat([[ 0.90796996 ,5.05836784],[-2.88425582 , 0.01687006],
                    [-3.3447423 , -1.01730512],[-0.32810867 , 0.48063528]
                    ,[ 1.90508653 , 3.530091  ]
                    ,[-3.00984169 , 2.66771831]
                    ,[-3.38237045 ,-2.9473363 ]
                    ,[ 2.22463036 ,-1.37361589]
                    ,[ 2.54391447 , 3.21299611]
                    ,[-2.46154315 , 2.78737555]
                    ,[-3.38237045 ,-2.9473363 ]
                    ,[ 2.8692781  ,-2.54779119]
                    ,[ 2.6265299  , 3.10868015]
                    ,[-2.46154315 , 2.78737555]
                    ,[-3.38237045 ,-2.9473363 ]
                    ,[ 2.80293085 ,-2.7315146 ]])
print(dataSet)
center, cluster = KMeans(dataSet, 2)
print('----')
print(center)
# [[-1.05990877 -2.0619207 ]
#  [-0.03469197  2.95415497]]
print('----')
print(cluster)
# [[ 1.          5.31632331]
#  [ 0.          7.6496132 ]
#  [ 0.          6.31168598]
#  [ 1.          6.20439303]
#  [ 1.          4.09444295]
#  [ 1.          8.93356179]
#  [ 0.          6.17778903]
#  [ 0.         11.26196081]
#  [ 1.          6.71620993]
#  [ 1.          5.917422  ]
#  [ 0.          6.17778903]
#  [ 0.         15.67457959]
#  [ 1.          7.1059799 ]
#  [ 1.          5.917422  ]
#  [ 0.          6.17778903]
#  [ 0.         15.36988591]]

python中kmeans的参数：

sklearn.cluster.KMeans(
    n_clusters=8,
    init='k-means++',
    n_init=10,
    max_iter=300,
    tol=0.0001,
    precompute_distances='auto',
    verbose=0,
    random_state=None,
    copy_x=True,
    n_jobs=1,
    algorithm='auto'
    )
n_clusters: 簇的个数，即你想聚成几类
init: 初始簇中心的获取方法
n_init: 获取初始簇中心的更迭次数，为了弥补初始质心的影响，算法默认会初始10个质心，实现算法，然后返回最好的结果。
max_iter: 最大迭代次数（因为kmeans算法的实现需要迭代）
tol: 容忍度，即kmeans运行准则收敛的条件
precompute_distances:是否需要提前计算距离，这个参数会在空间和时间之间做权衡，如果是True 会把整个距离矩阵都放到内存中，auto 会默认在数据样本大于featurs*samples 的数量大于12e6 的时候False,False 时核心实现的方法是利用Cpython 来实现的
verbose: 冗长模式（不太懂是啥意思，反正一般不去改默认值）
random_state: 随机生成簇中心的状态条件。
copy_x: 对是否修改数据的一个标记，如果True，即复制了就不会修改数据。bool 在scikit-learn 很多接口中都会有这个参数的，就是是否对输入数据继续copy 操作，以便不修改用户的输入数据。这个要理解Python 的内存机制才会比较清楚。
n_jobs: 并行设置
algorithm: kmeans的实现算法，有：’auto’, ‘full’, ‘elkan’, 其中 ‘full’表示用EM方式实现
虽然有很多参数，但是都已经给出了默认值。所以我们一般不需要去传入这些参数,参数的。可以根据实际需要来调用。

•基于密度的方法;

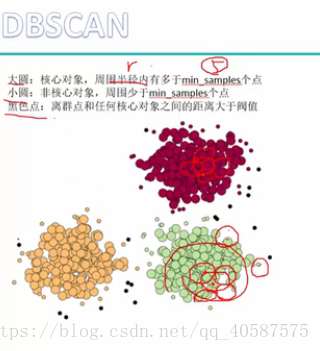
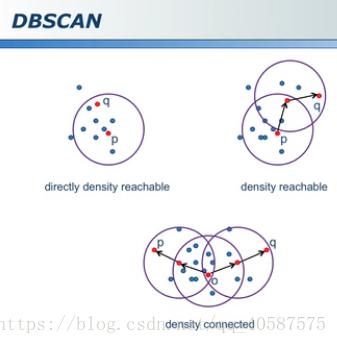
•DBSCAN （需要指定半径，对离群点的寻找作用很大）:

•大圆：核心对象，周围半径内有多于min_samples 个点

•小圆：非核心对象，周围少于 min_samples 个点

•黑色点：离群点和任何核心对象之间的距离大于阈值

​​

参考：https://blog.csdn.net/taoyanqi8932/article/details/53727841