【NLP_Stanford课堂】最小编辑距离

一、什么是最小编辑距离

最小编辑距离：是用以衡量两个字符串之间的相似度，是两个字符串之间的最小操作数，即从一个字符转换成另一个字符所需要的操作数，包括插入、删除和置换。

每个操作数的cost：

每个操作数的cost一般是1
如果置换的cost是2，而插入和删除的cost是1，我们称之为Levenshtein 距离。

作用：

计算衡量机器翻译和语音识别的好坏：将机器得到的字符串与专家写的字符串比较最小编辑距离，以一个单词为一个单位。
命名实体识别和链接：比如通过计算最小编辑距离，可以判定IBM.Inc和IBN非常相似，只有一个单词不同，所以认为这是指向同一个命名实体。

二、如何找到最小编辑距离

实质：寻找一条从“开始字符串”到“最终字符串”的路径（一个操作序列）

具体过程：

初始状态：机器翻译出来的单词
操作：插入、删除、置换
黄金状态：我们尽力希望得到的单词
路径花费：操作数目，要求最小化
实例：
单词intention通过删除i可以得到ntention，通过插入e可以得到eintention，通过将i换成e可以得到entention。以上从intention到叶子节点的任意一个单词经过的操作数就是一条路径。
可以发现枚举出所有可转变成的单词的花费是十分巨大的，我们不可能用枚举遍历的方式来寻找一条最短路径，一种解决方法是：使用剪枝
每层中有很多路径被剪枝了，只在每一层中保留最短的那条路径

定义：

设有两个字符串：X和Y。其中X长度为n，Y长度为m
定义D(i,j)，表示
- X[1..i]和Y[]1..j]之间的编辑距离，
- 从而X和Y之间的编辑距离为D(n,m)

三、如何计算中间距离D(n,m)

基准方法：动态规划从i=0，j=0

具体算法：

初始X的长度为i，则Y的长度为0时，需要在Y中插入i个字符才能使Y变成X，所以D(i,0)=i；同理X的长度为0，Y的长度为j时，需要删去j个字符才能使Y变成X，所以D(0,j)=j.

环条件：三个式子分别对应在i-1的基础上删除一个字符使之变成j、在j-1的基础上插入1个字符使之变成i和置换这三个操作，其中若X(i)=Y(j)，则无需置换，所以cost等于1，否则需要各在i-1和j-1上插入一个字符，cost等于2

计算实例：

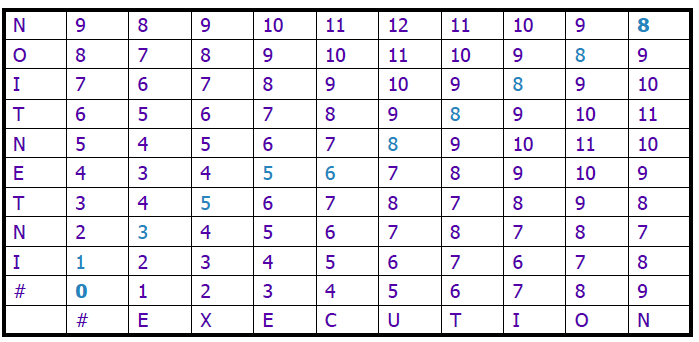
四、如何回溯计算两个字符串之间对齐的字符

在上一步计算矩阵的过程中，加入方向，具体可参考《算法导论》中的寻找最长公共子序列

计算实例：

五、带权重的最短距离

权重：指插入、删除和置换三种操作有不同的权重，不再简单都认为cost是1

原因：

拼写校正：有些单词通常更容易被拼错，比如根据统计e非常容易被拼错成a
生物学：某几种插入或删除更容易出现

经过调整的算法如下：

注：使用Levenshtein距离

六、计算生物学上的最小编辑距离（相似度）

问题：找到以下两个序列中的对齐序列，其可能是核苷酸或者蛋白质的结构

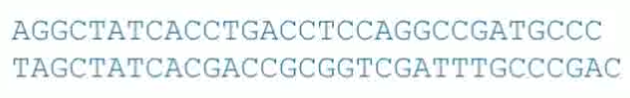
要求得到以下对齐序列：

在NLP上，我们称之为最小距离，而在计算生物学上，我们称之为相似度

算法：Needleman-Wunsch 算法

其中d表示插入和删除的cost，s表示置换的positive value

1. 变形一

特殊情况：两个字符串的头尾没有对齐，只有中间一部分重合

具体可能有两种情形：

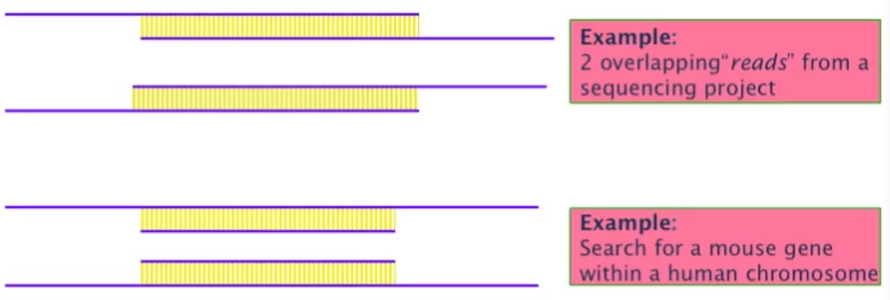
要求：检测重叠部分中的相似度，即重叠检测问题

算法：

注：调整算法开始的起点和终点

2. 变形二

要求：要求找到两个字符串中相似度最大的序列，可以有多个，即局部对齐问题

实例：要求找到以下cccggg的部分

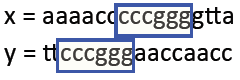
算法：Smith-Waterman算法

计算实例：

结果：

其中找到两个最大局部对齐序列

一是ATCAT和ATTAT的相似度为3，其中A与A相等，得一分；T与T相等，得一分；T与C不相等，要删除，所以减一分；A与A相等，得一分；T与T相等，得一分

二是ATC和ATC的相似度也为3。