Logistic回归基础篇之梯度上升算法

代码示例：

import numpy as np
import matplotlib.pyplot as plt

def loadDataSet():
    dataMat = [];labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    fr.close()
    return dataMat,labelMat

def sigmoid(intX):
    return 1.0/(1+np.exp(-intX))

def gradAscent(dataMatIn,classLabels):
    dataMatrix = np.mat(dataMatIn)
    labelMat = np.mat(classLabels).transpose()
    m,n = np.shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = np.ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        error = labelMat - h
        weights += alpha * dataMatrix.transpose() * error
    return weights

def plotBestFit(weights):
    dataMat,labelMat = loadDataSet()
    dataArr = np.array(dataMat)
    n = np.shape(dataArr)[0]
    xcord1 = [];ycord1 = []
    xcord2 = [];ycord2 = []
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]);ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]);ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')
    ax.scatter(xcord2,ycord2,s=30,c='green')
    x = np.arange(-3.0,3.0,0.1)
    y = (-weights[0] - weights[1]*x)/weights[2]
    ax.plot(x,y)
    plt.xlabel('X1');plt.ylabel('X2')
    plt.show()

if __name__ == '__main__':
    dataMat,labelMat = loadDataSet()
    weights = gradAscent(dataMat,labelMat)
    plotBestFit(weights)

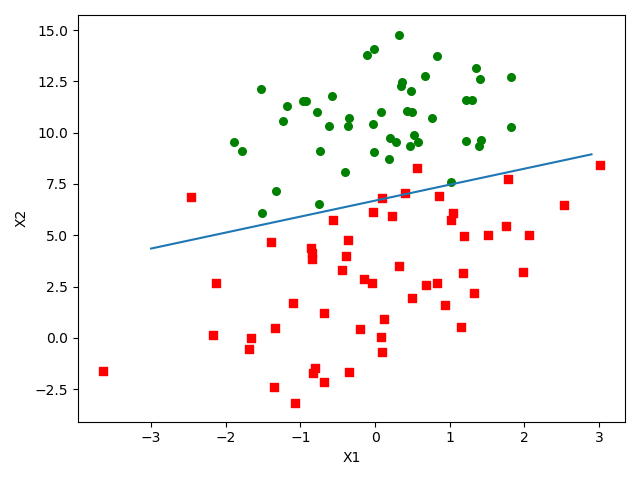
运行结果：

参考博客：https://cuijiahua.com/blog/2017/11/ml_6_logistic_1.html