奇异值分解(SVD)(基础知识)
参考:https://www.cnblogs.com/pinard/p/6251584.html
参考:http://blog.csdn.net/u010099080/article/details/68060274
参考:https://www.zhihu.com/question/22237507
定义:
SVD用于对矩阵进行分解,假设待分解矩阵A大小为m×n的矩阵,那么矩阵A的SVD为:
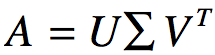
以上的U是一个mxm的矩阵,Σ是一个mxn的矩阵,除了主对角线意外其他值均为0,主对角线上每个元素均为奇异值,V是一个nxn的矩阵,且U和V均满足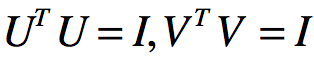 .
.
下面则介绍如何求得U、Σ、V的过程。
我们将A的转置和A作矩阵相乘,那么得到nxn的方阵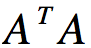 ,由于这是一个方阵,那么我们可以进行特征分解,得到特征值和特征向量满足下式子:
,由于这是一个方阵,那么我们可以进行特征分解,得到特征值和特征向量满足下式子:
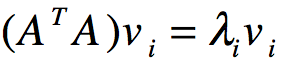
这样我们则得到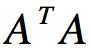 的特征值和对应的特征向量,将特征向量组成一个nxn的矩阵,那么就得到SVD公式的V矩阵,一般将V的每个特征向量叫做A的右奇异向量。
的特征值和对应的特征向量,将特征向量组成一个nxn的矩阵,那么就得到SVD公式的V矩阵,一般将V的每个特征向量叫做A的右奇异向量。
若将A和A的转置作矩阵相乘,那么得到mxm的矩阵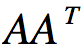 ,同样进行特征分解,得到如下的特征值和特征向量:
,同样进行特征分解,得到如下的特征值和特征向量:
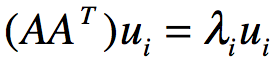
这样则得到对应的m个特征向量u和m个特征值,将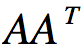 的所有特征向量组成一个mxm的特征矩阵U,那么就能得到SVD矩阵里的U矩阵,一般我们将U中的每个特征向量称为A的左奇异向量。
的所有特征向量组成一个mxm的特征矩阵U,那么就能得到SVD矩阵里的U矩阵,一般我们将U中的每个特征向量称为A的左奇异向量。
剩下的求奇异值矩阵Σ过程,由于其除了对角线上的奇异值之外其他都是0,那么我们只需要求出对应的奇异值σ即可。
由于:
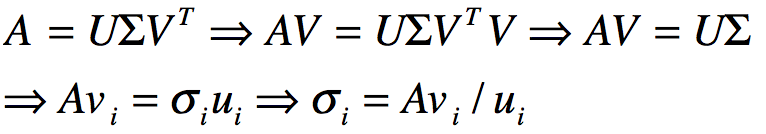
那么我们就可以得到各奇异值,进而得到奇异矩阵Σ.
判断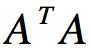 和
和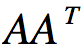 得到的特征向量组成的矩阵分别为V矩阵和U矩阵,以如下为例(ΣT=Σ):
得到的特征向量组成的矩阵分别为V矩阵和U矩阵,以如下为例(ΣT=Σ):
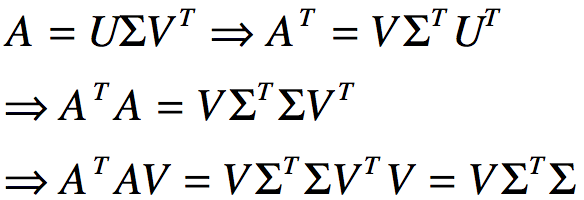
从而发现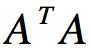 的特征向量组成的就是SVD分解中的V矩阵,进一步可以发现特征值矩阵为奇异值矩阵的平方,即得到奇异值和特征值满足关系
的特征向量组成的就是SVD分解中的V矩阵,进一步可以发现特征值矩阵为奇异值矩阵的平方,即得到奇异值和特征值满足关系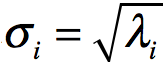 ,同理可以得到
,同理可以得到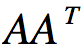 的特征向量组成的就是SVD分解中的U矩阵。
的特征向量组成的就是SVD分解中的U矩阵。
由于奇异值和我们特征分解中的特征值类似,在奇异值矩阵中同样是从大到小排序,且奇异值减小速度非常快,在很多情况下,少量的奇异值之和能占全部奇异值之和的较高的比例,因而我们用最大的k个奇异值及对应的左右奇异向量来近似描述矩阵,即有如下表示:
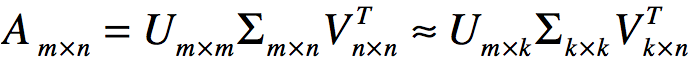
其中k比n小很多,即大的矩阵A可以分解为3个小的矩阵来表示。
由于如上性质,SVD分解可以用于PCA降维,可以用来数据压缩和降噪,也可以用于推荐算法,将用户和喜好对应的矩阵作特征分解,进而得到隐含的用户需求来做推荐。
SVD在PCA中的应用:
具体可以参考:https://www.cnblogs.com/pinard/p/6251584.html 中对PCA的讲解
在PCA原理中,提到PCA降维,需要找到样本协方差矩阵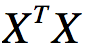 中最大的d个特征向量,然后将这d个最大的特征向量组成矩阵来作低维投影降维,在这个过程中需要先求出协方差矩阵
中最大的d个特征向量,然后将这d个最大的特征向量组成矩阵来作低维投影降维,在这个过程中需要先求出协方差矩阵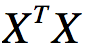 ,当样本数和特征数都很多的时候计算量会比较大。
,当样本数和特征数都很多的时候计算量会比较大。
由于有些SVD的实现算法可以不先求出对应的协方差矩阵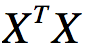 ,也可以得到对应的右奇异矩阵V,即我们不需要对PCA算法做特征分解,而是通过做SVD来完成,该方法在样本量较大的时候比较有效,其中scikit-learn的PCA算法背后真正实现的是SVD算法。
,也可以得到对应的右奇异矩阵V,即我们不需要对PCA算法做特征分解,而是通过做SVD来完成,该方法在样本量较大的时候比较有效,其中scikit-learn的PCA算法背后真正实现的是SVD算法。
另一方面,PCA仅使用了SVD的右奇异矩阵,并没有使用左奇异矩阵。那么左奇异矩阵的作用在于:
假设我们的样本是m x n 的矩阵X,我们通过SVD分解得到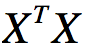 最大的d个特征向量组成的m x d维矩阵U,那么我们通过如下处理:
最大的d个特征向量组成的m x d维矩阵U,那么我们通过如下处理:
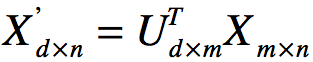
可以得到d x n的矩阵X‘,这个矩阵和我们原来m x n维的样本矩阵X相比,行数从原来的m减少到了d,从而对行数进行压缩,也就是说左奇异矩阵用于对行数压缩,右奇异矩阵用于对列数进行压缩,也就是PCA降维。
例子:
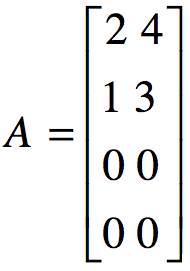 计算得:
计算得:
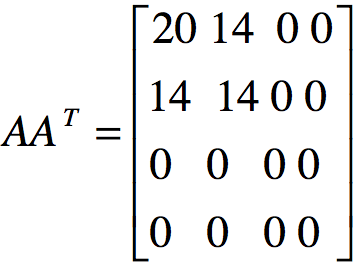
根据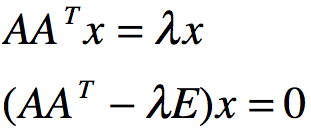 ,得到特征值
,得到特征值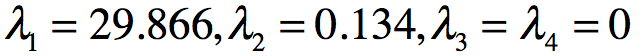
从而得到单位化的特征矩阵U为:
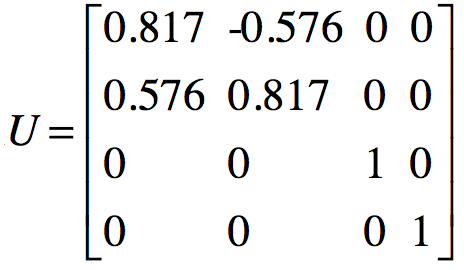
同理求解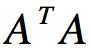 的特征值和特征向量,将特征值降序排列之后得到单位化的特征向量矩阵V为:
的特征值和特征向量,将特征值降序排列之后得到单位化的特征向量矩阵V为:
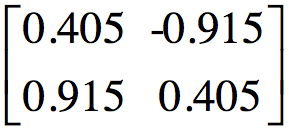
根据特征值的平方根得到对角矩阵:
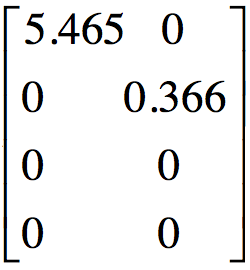
到此,矩阵A通过SVD分解得到:
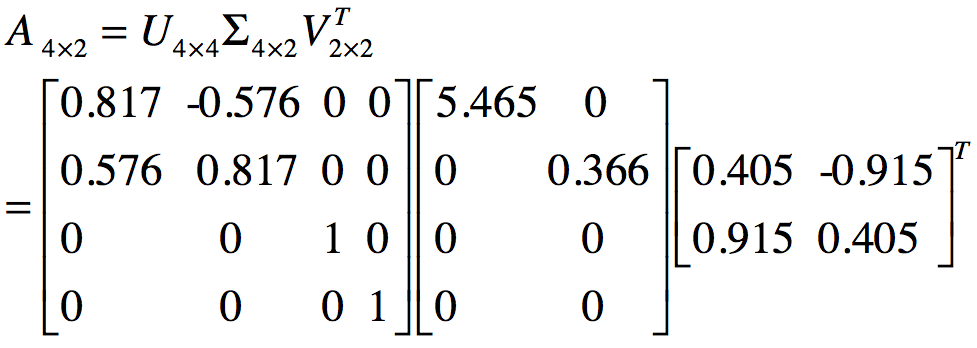
奇异值分解(SVD)(基础知识)的更多相关文章
- 强大的矩阵奇异值分解(SVD)及其应用
版权声明: 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@gm ...
- 机器学习中的数学-矩阵奇异值分解(SVD)及其应用
转自:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html 版权声明: 本文由LeftNotE ...
- 机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用
版权声明: 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@gm ...
- Matlab - 基础知识
Matlab R2016a完全自学一本通 记在前面: (1)函数中:dim=1 按列:dim=2 按行 (2)这本书很垃圾,不建议买. (3)在数据库连接中,用两个单引号表示字符串,千万不能用双引号 ...
- 强大的矩阵奇异值分解(SVD)
转:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html 前言: PCA的实现一般有两种,一种 ...
- 奇异值分解(SVD)原理及应用
一.奇异值与特征值基础知识: 特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法.两者有着很紧密的关系,我在接下来会谈到,特征值分解和奇异值分解的目的都是一样,就是提取出一个矩阵最重要的特征. ...
- 矩阵奇异值分解(SVD)
转自:https://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html (感谢,讲解的太好了) 在机器 ...
- 机器学习中的数学-强大的矩阵奇异值分解(SVD)及其应用
版权声明: 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@gm ...
- 奇异值分解SVD
在介绍奇异值分解(SVD)之前我们先来回顾一下关于矩阵的一些基础知识. 矩阵基础知识 方阵 给定一个$ n×m $的矩阵$ A $,若n和m相等也就是矩阵的行和列相等那矩阵$ A $就是一个方阵. 单 ...
随机推荐
- 20160513--js 弹出窗口带有iframe控件 备忘
需要引用JQuery. /*! * 主 题:<页面弹出窗口> * 说 明:用于页面弹出的窗口. * 功能描述: * 1.生成弹出窗口,窗口内包括iframe控件: * 2.窗口弹出时,生成 ...
- 重拾SQL——表中索值
2016.10.23 + 2016.11.02 1.选择所有数据(查看整表) MariaDB [tianyuan]> select * from pet; +----------+------- ...
- Bootstrap 学习笔记 项目实战 首页内容介绍 下
最终效果: HTML代码 <!DOCTYPE html> <html lang="zh-cn"> <head> <meta charset ...
- The bean 'dataSource', defined in BeanDefinition defined in class path resou
SpringCloud对应SpringBoot不匹配 Greenwich 2.1.x Finchley 2.0.x Edgware 1.5.x Dalston 1.5.x SpringBoot Spr ...
- css-sprite 雪碧图的使用,合并多张小图,背景图片当按钮的设置
背景图片基础: 使用background-image来设置背景图片 语法: background-image:url(相对与css的路径) 如果背景图片大于元素,默认会显示图片的左上角 如果背景图片和 ...
- 数组方法之reduce实践
Array.prototype.reduce let arr = [1, 2, 3, 4], sum = arr.reduce((prev, curr, index, arr) => { ret ...
- 知乎使用selenium反爬虫的解决方案
from selenium.webdriver import Chrome from selenium.webdriver import ChromeOptions option = ChromeOp ...
- 将图片地址转为blob格式的例子
HTML代码: <div id="forAppend" class="demo"></div> Javascript代码: <sc ...
- Java Web项目使用图形验证码 — Kaptcha
一.验证码介绍 生成的主要方式: 1.使用Java原生的方式,其中包含了Servlet.AWT.ImageIO的使用: 2.使用开源库,例如Jcaptcha.Kaptcha...: (各图形验证码开源 ...
- mysql中explain输出列之id的用法详解
参考mysql5.7 en manual,对列id的解释: The SELECT identifier. This is the sequential number of the SELECT wit ...
