清北学堂清华大学钟皓曦神仙讲课day3摘要

---恢复内容开始---

今天全是DP

awsl，真的好难

先从斐波那契开始：

dp：满足有一个状态边界条件（f[0]=0,f[1]=1）

边界条件：不需要计算其他状态的值而可以直接得出的状态或者最底层状态（不能由其他状态推出来）

然后是状态转移方程：f[n]=f[n-1]+f[n-2](然后是矩阵加速或者递推。。)

总之：边界条件，状态，转移方程为三大核心（其他都是一些题目变量。）

据说动态规划和dag（大哥）是等价的，但是图论后几天再讲。。QWQ

DP有这几种：（zhx大佬的神仙字体）

这是斐波那契数列顺推：

用别人更新自己。

逆推：

用自己更新别人。

记忆化搜索：

复杂度O（f[n]）f[n]为第n项的值

其实他有通项公式的：

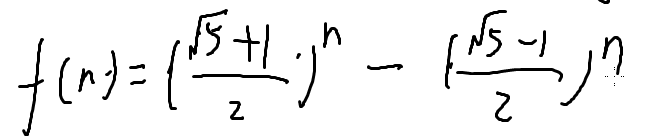
也就是说，复杂度为指数级别，因为右边那一项小于1，他的n次方也小于一

为何如此之慢？

因为他有重复调用（f[n]=f[n-1]+f[n-2],f[n-1]=f[n-2]+f[n-3]）f[n-2]被调用两次

那么我们再开一个数组，用来判断f[n]是否被算过（suan_le_mei数组）

算过就是1，否则为0（bool）

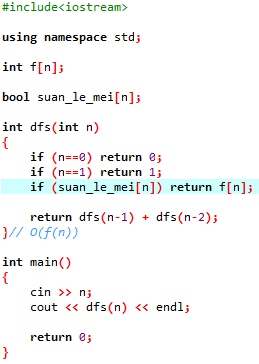
也就是判断是否被算过（f[n]已经有值了），算过就直接返回，没算过就1.算2.赋值bool3.赋值f[n]

没错就是这样QWQ（%zhx大佬竟然把蒟蒻讲明白了）

在安利一下本人写的斐波那契矩阵加速：https://www.cnblogs.com/lbssxz/p/10679655.html

例题完结

常见dp种类：

其他dp好可怕（最可怕的是未知）

还有两种NOIP涉及概率比较小的：

但是其他4种dp套路要背熟。

1，数位dp：

给定两个正整数l,r，求l到r有多少个数？

（wtf这个题不是r-l+1吗）

但是，zhx让你用数位dp做。

首先将题目转化一下（减去l）得0到x有多少个数这个问题

那么设0<=v<=x,将v按十进制位数分解，得每一位vn,vn-1,vn-2....v1,我们从高位开始填v的位数，要分两种情况：

1，当前面已经填好的位数和x对应位数相同时，现在填的位数必须小于等于x对应位数才满足v<=x

2，当前面有至少一位和x对应位数不相同时，这意味着当前一位不管填多少，都满足v<x,那么，0到9随便填就行，

状态：设数组f[i][j],代表当前填到了第i位，j的值为（0:当前面几位有至少一位不和x对应位相等时，随便填　　1:当前面几位都相同时只能填vi<=x[i]）

状态转移：从第一位开始，if分两种情况递归

代码：先存x的位数：

其中z为存x位数的数组（下标从0开始）

然后是dp主体部分：

首先必须清空memset()%

初始化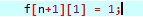：why？因为他们在n+1位的值都为0，所以相等的情况只有一种

然后用一个for循环，枚举从第n位到第0位，然后分情况转移就ok了。QWQ

改一下问题：求l,r区间内有多少个相邻数位只差大于2的数？

状态为了包含所有条件，发生了变化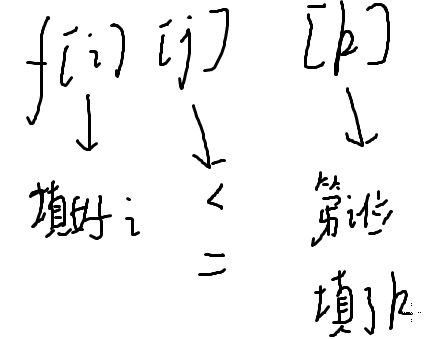

其他改改就行。

2.树形dp

给你一个有n个结点的树，求它有几个点（没错答案就是n你没看错）

老师竟然把这么简单的题让我们用树形dp做

又变难了

#include<iostream>

using namespace std;

int f[];

void dfs(int p)
{
    for (x is p's son)
    {
        dfs(x);
        f[p] += f[x];
    }
    f[p] ++;
}

int main()
{
    cin >> n;
    read_tree();

    dfs();
    cout << f[] << endl;

    return ;
}

状态dp

状压复杂度为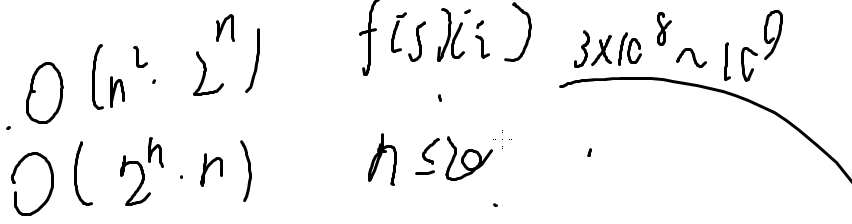

而n<=20时为状压的数据范围，考虑使用状压