R语言预测实战（第一章）

本例使用forecast包中自带的数据集wineind，它表示从1980年1月到1994年8月，

由葡萄酒生产商销售的容量不到1升的澳大利亚酒的总量。数据示意如下：

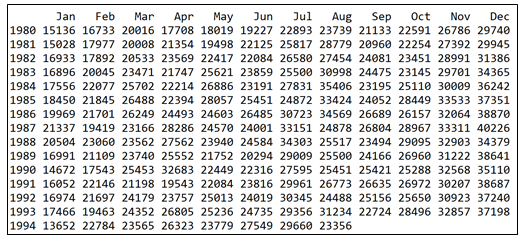
#观察曲线簇
len=1993-1980+1
data0=wineind[1:12*len]
range0=range(data0)+c(-100,100)
plot(1:12,1:12,ylim=range0,col='white',xlab="月份",ylab="销量")
for(i in 1:len)
{
  points(1:12,wineind[(12*(i-1)+1):(12*i)])
  lines(1:12,wineind[(12*(i-1)+1):(12*i)],lty=2)
}

#对数据按指定格式进行转换

Month=NULL
DstValue=NULL
RecentVal1=NULL
RecentVal4=NULL
RecentVal6=NULL
RecentVal8=NULL
RecentVal12=NULL
#替换掉太大或太小的值

wineind[wineind<18000]=18000
wineind[wineind>38000]=38000
for(i in (12+1):(length(wineind)-1))
{
  Month<-c(Month,i%%12+1)
  DstValue<-c(DstValue, wineind[i+1])
  RecentVal1<-c(RecentVal1,wineind[i])
  RecentVal4<-c(RecentVal4,wineind[i-3])
  RecentVal6<-c(RecentVal6,wineind[i-5])
  RecentVal8<-c(RecentVal8,wineind[i-7])
  RecentVal12<-c(RecentVal12,wineind[i-11])
}
preData=data.frame(Month,DstValue,RecentVal1,RecentVal4,RecentVal6,RecentVal8,RecentVal12)
head(preData)
##Month DstValue RecentVal1 RecentVal4 RecentVal6 RecentVal8 RecentVal12

## 1     2    18000      18000      22591      23739      19227       18000
## 2     3    20008      18000      26786      21133      22893       20016
## 3     4    21354      20008      29740      22591      23739       18000
## 4     5    19498      21354      18000      26786      21133       18019
## 5     6    22125      19498      18000      29740      22591       19227
## 6     7    25817      22125      20008      18000      26786       22893
#画出散点矩阵图
plot(preData)

#使用DstValue与RecentVal12拟合线性模型
lm.fit=lm(DstValue~RecentVal12,data=preData)
cook<-cooks.distance(lm.fit)  #通过cooks.distance函数计算每行记录对模拟的影响度量
plot(cook)
abline(h=0.15,lty=2,col='red')

cook[cook>0.15]
preData=preData[-c(123,79),]

#根据上一步输出的基础数据，提取150行作为训练数据，剩下的做测试数据
#分离训练集与测试集
trainData=preData[1:150,]
testData=preData[151:163,]

#建立模型
lm.fit<-lm(DstValue ~ Month + RecentVal1 + RecentVal4 +
             RecentVal6 + RecentVal8 + RecentVal12,data=trainData)
summary(lm.fit)

#在所有的非线性方法中，多项式比较适合单个变量的衍生变换

#对Month、RecentVal4、RecentVal8三个变量按5次多项式进行衍生
lm.fit<-lm(DstValue~Month+I(Month^2)+I(Month^3)+I(Month^4)+
             I(Month^5)+RecentVal1+RecentVal4+I(RecentVal4^2)+
             I(RecentVal4^3)+I(RecentVal4^4)+I(RecentVal4^5)+
             RecentVal6+RecentVal8+I(RecentVal8^2)+I(RecentVal8^3)+
             I(RecentVal8^4)+I(RecentVal8^5)+RecentVal12,data=trainData)
summary(lm.fit)

#由于涉及到变量太多，使用逐步回归删除掉影响小的变量
lm.fit<-step(lm.fit)
summary(lm.fit)

#去掉P值较大的三个变量I(RecentVal4^3)、I(RecentVal4^4)、
#I(RecentVal4^5)后，再拟合一次模型

lm.fit<-lm(formula=DstValue~Month+I(Month^4)+I(Month^5)+RecentVal6+
             RecentVal8+I(RecentVal8^2)+I(RecentVal8^3)+I(RecentVal8^4)+
             I(RecentVal8^5)+RecentVal12,data=trainData)
#lm.fit就是我们建立的用于时间序列预测的线性回归模型
summary(lm.fit)

#预测及误差分析
#用lm.fit作为预测模型，对预测数据源testData进行预测
#对新数据进行预测
testData$pred=predict(lm.fit,testData)
#计算百分误差率
testData$diff=abs(testData$DstValue-testData$pred)/testData$DstValue
testData
summary(testData)