hdu多校第二场1008（hdu6598） Harmonious Army 最小割

题意：

一个军队有n人，你可以给他们每个人安排战士或者法师的职业，有m对人有组合技，组合技的信息是a,b,c，代表如果这两个人是两个战士，则组合技威力为a，一个战士一个法师，威力为b，其中b=a/4+c/3，两个法师，威力为c，求最大的威力。

题解：

这道题给出了一个最小割的清奇思路。

首先不去想边权，只想连通性，设源点为战士，汇点为法师，中间的点记为军队中的人，人和源点汇点之间连边，有组合技的人两两之间连边，简单起见，从只有两个人的情况讨论，这张图割完了只能是如下形式：

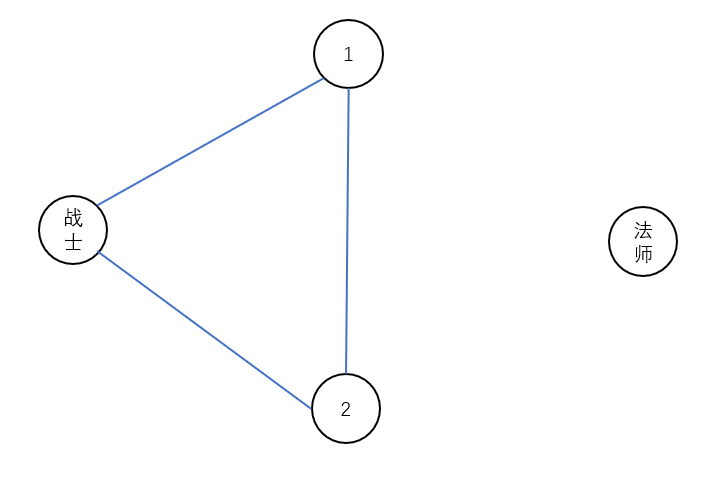
（两个战士）

（两个法师）

（1战士2法师）

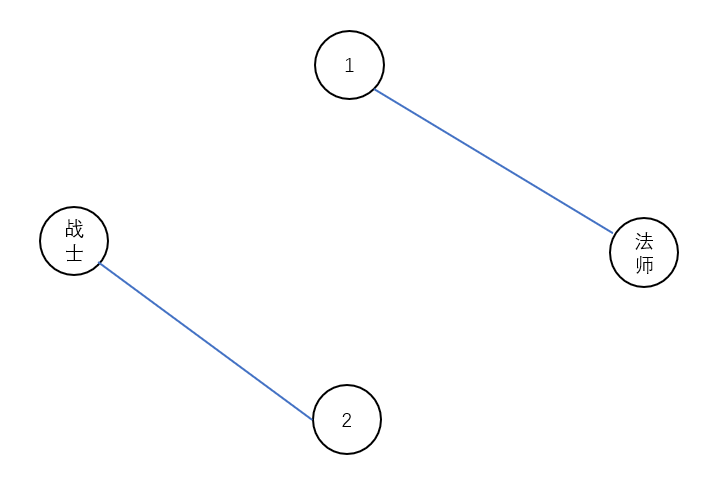
（1法师2战士）

我们假想，求出了最小割，说明了每个人只选一种职业后的情况。那么，被割掉的，应该是这两个人选择其他职业的威力之和。

那么，边权怎么算呢？

可列出如下方程组

（源，1）+（源，2）=b+c

（源，1）+（2，汇）+（1，2）=（1，汇）+（源，2）+（1，2）=a+c

（1，汇）+（2，汇）=a+b

得到一组解

（源，1）=（源，2）=(a+b)/2

（1，汇）=（2，汇）=(c+b)/2

（1，2）=(a-2b+c)/2

以此建边，重复的边就是权值之和，求出最小割后，用所有职业组合的威力之和减去最小割，就是答案。

注意，题目数据保证了上述值都为正，但是做类似题时思路时不要僵化，必须是上述方程组解为正时才可应用此法。

#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define rep(i, a, b) for(int i=(a); i<(b); i++)
#define per(i, a, b) for(int i=(b)-1; i>=(a); i--)
#define sz(a) (int)a.size()
#define de(a) cout << #a << " = " << a << endl
#define dd(a) cout << #a << " = " << a << " "
#define all(a) a.begin(), a.end()
#define pw(x) (1ll<<(x))
#define lb(x) ((x) & -(x))
#define endl "\n"
typedef double db;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef vector<int> vi;
const int P = 1e9 + ;
int add(int a, int b) {if((a += b) >= P) a -= P; return a <  ? a + P : a;}
int mul(int a, int b) {return 1ll * a * b % P;}
int kpow(int a, int b) {int r=;for(;b;b>>=,a=mul(a,a)) {if(b&)r=mul(r,a);}return r;}
//----

const int N = 1e3 + ;
const db eps = 1e-;
template<class T>
struct Dinic{
    const static int N =  , M = N * ;
    int s , t , n , h[N] , cur[N] , lv[N] , q[N] , e , ne[M] , to[M];
    T cap[M] , flow;
    void liu(int u,int v,T w){ to[e] = v;ne[e] = h[u];cap[e] = w;h[u] = e++;}
    void link(int u,int v,T w){ liu(u , v , w);liu(v , u , );}
    void ini(int _n = N) { fill(h , h + (n=_n) , -);e = ;}
    bool bfs(){
        int L =  , R = ;
        fill(lv , lv + n , -);
        lv[q[R++] = s] = ;
        while(L < R && !~lv[t]){
            int c = q[L++];
            for(int k = h[c]; ~k ; k = ne[k])
                if(cap[k] >  && !~lv[to[k]])
                    lv[q[R++] = to[k]] = lv[c] + ;
        }
        return ~lv[t];
    }
    T dfs(int c,T mx){
        if(c == t) return mx;
        T ret = ;
        for(int &k = cur[c]; ~k; k = ne[k]){
            if(lv[to[k]] == lv[c] +  && cap[k] > ){
                T flow = dfs(to[k] , min(mx , cap[k]));
                ret += flow;cap[k] -= flow , cap[k^] += flow;mx -= flow;
                if (!mx) return ret;
            }
        }
        lv[c] = -;
        return ret;
    }
    T run(int _s,int _t){
        s = _s , t = _t;
        flow = ;
        while(bfs()){
            copy(h , h + n , cur);
            flow += dfs(s, ~0U>>);
        }
        return flow;
    }
};

Dinic<db> G; 

ll n, m, s, t, u, v, a, b, c, ans, w[N], ww[N];

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie();

    while (cin >> n >> m) {
        ans=;
        rep(i,,n+) w[i]=ww[i]=;

        G.ini(n + ); s = G.n - ; t = s + ;
        rep(i, , m+) {
            cin >> u >> v >> a >> b >> c;
            w[u] += a + b; w[v] += a + b;
            ww[u] += b + c; ww[v] += b + c;
            G.link(u, v, - b + a / 2.0 + c / 2.0);
            G.link(v, u, - b + a / 2.0 + c / 2.0);
            if (u > v) swap(u, v);
            ans += a + c + b;
        }
        rep(i, , n+) G.link(s, i, w[i] / 2.0), G.link(i, t, ww[i] / 2.0);
        ans = (ll)round(ans - G.run(s, t));
        cout << ans << endl;
    }

    return ;
}