6364. 【NOIP2019模拟2019.9.20】养马

题目描述

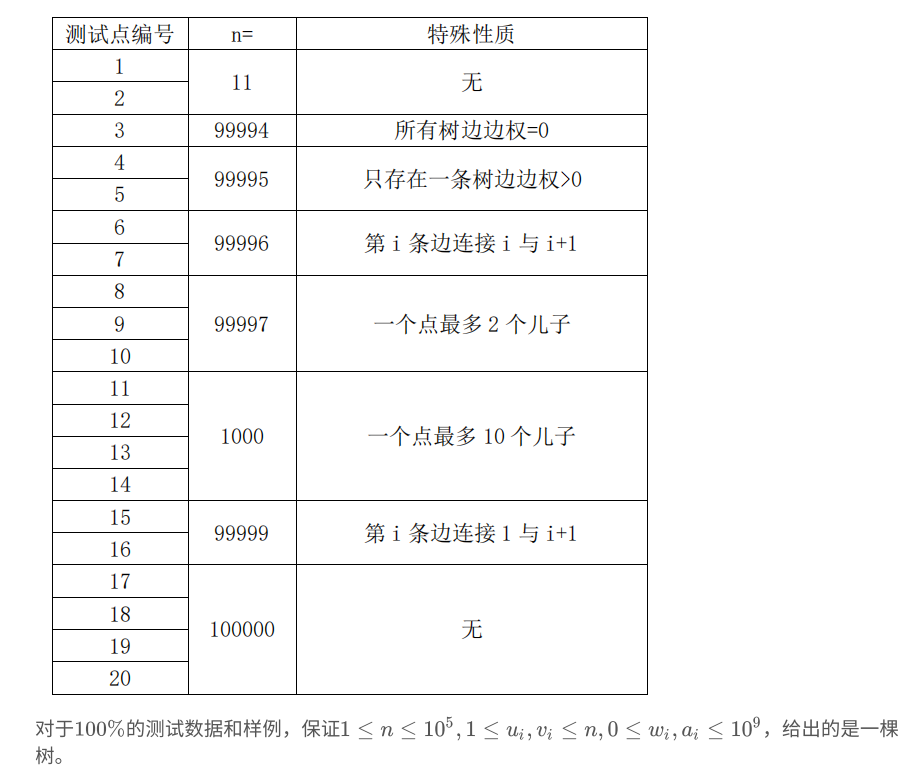
题解

一种显然的水法：max(0,-(点权-边权之和*2))

这样会挂是因为在中途体力值可能会更小，所以考虑求走完每棵子树所需的至少体力值

---

考虑从子树往上推求出当前点的答案

设每棵子树从根往下走的所需体力值为f，走完的贡献为sum

由于要加上 当前点-->儿子 这条边，所以实际上走完的贡献sum'=sum-边权*2

所需的体力值f'=max(边权+f,2*边权-sum)，这里其实有两种情况

①当前点-->儿子-->子树（-->儿子），那么最坏情况就是(子树的最坏情况+边权)

②当前点-->儿子-->子树-->儿子-->当前点，最终的贡献实际为sum-边权*2，那么就需要至少max(0,边权*2-sum)的体力

---

显然对于贡献≥0的点按照需求从小到大取

对于贡献<0的点，定义减少量=-贡献

那么按照需求-减少量从大到小排序即可

证明：

定义差值=需求-减少量

对于两个儿子，设第一个儿子的差值和减少量分别为a和b，第二个为cd

先假设已经按照差值排序，且排序后两个儿子相邻，那么有a≥c

证明交换后不会更优

设x为走这两棵子树前的体力，保证在中途不会出现负数且能达到需求量

那么有

交换前：

x≥a+b,x-b≥c+d

交换后：

x≥c+d,x-d≥a+b

根据式子

根节点贡献+恢复的体力-每棵子树的减少量之和=剩余体力，其中只有恢复的体力是变量，所以可以发现剩余体力越少=答案越小

由于交换前后剩余的体力都是x-b-d，所以要使x尽量小（太大可能会导致有剩余）

所以变成证明

max(a+b,b+c+d)≤max(c+d,a+b+d)

由于a+b+d≤max(c+d,a+b+d)，且a+b+d≥a+b和b+c+d（a≥c），所以max(a+b,b+c+d)≤a+b+d≤max(c+d,a+b+d)

得证

code

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
using namespace std;

struct type{
	long long f,sum;
} b[100001],c[100001];
int a[200001][3];
int ls[100001];
int w[100001];
long long f[100001];
long long sum[100001];
int n,i,j,k,l,len;
long long ans;

bool cmp(type a,type b)
{
	return a.f<b.f;
}
bool Cmp(type a,type b)
{
	return a.f-a.sum>b.f-b.sum;
}

void New(int x,int y,int z)
{
	++len;
	a[len][0]=y;
	a[len][1]=ls[x];
	a[len][2]=z;
	ls[x]=len;
}

void dfs(int Fa,int t)
{
	int i,l1=0,l2=0;
	long long now=w[t];

	sum[t]=w[t];

	for (i=ls[t]; i; i=a[i][1])
	if (a[i][0]!=Fa)
	{
		dfs(t,a[i][0]);
		sum[t]+=sum[a[i][0]]-a[i][2]-a[i][2];
	}

	if (!ls[t]) return;

	for (i=ls[t]; i; i=a[i][1])
	if (a[i][0]!=Fa)
	{
		if (sum[a[i][0]]-a[i][2]-a[i][2]>=0)
		{
			++l1;
			b[l1].f=max(f[a[i][0]]+a[i][2],-(sum[a[i][0]]-a[i][2]-a[i][2]));
			b[l1].sum=sum[a[i][0]]-a[i][2]-a[i][2];
		}
		else
		{
			++l2;
			c[l2].f=max(f[a[i][0]]+a[i][2],-(sum[a[i][0]]-a[i][2]-a[i][2]));
			c[l2].sum=-(sum[a[i][0]]-a[i][2]-a[i][2]);
		}
	}

	if (l1)
	{
		sort(b+1,b+l1+1,cmp);
		fo(i,1,l1)
		{
			if (now<b[i].f)
			{
				f[t]+=b[i].f-now;
				now=b[i].f;
			}
			now+=b[i].sum;
		}
	}
	if (l2)
	{
		sort(c+1,c+l2+1,Cmp);
		if (now<(c[1].f-c[1].sum))
		{
			f[t]+=(c[1].f-c[1].sum)-now;
			now=0;
		}
		else
		now-=(c[1].f-c[1].sum);

		fo(i,1,l2)
		{
			if (i>1)
			now+=(c[i-1].f-c[i-1].sum)-(c[i].f-c[i].sum);

			if (now<c[i].sum)
			{
				f[t]+=c[i].sum-now;
				now=c[i].sum;
			}
			now-=c[i].sum;
		}
	}
}

int main()
{
//	freopen("a.in","r",stdin);
//	freopen("b.out","w",stdout);
	freopen("horse.in","r",stdin);
	freopen("horse.out","w",stdout);

	scanf("%d",&n);
	fo(i,1,n)
	scanf("%d",&w[i]);
	fo(i,2,n)
	{
		scanf("%d%d%d",&j,&k,&l);

		New(j,k,l);
		New(k,j,l);
	}

	dfs(0,1);

	printf("%lld\n",f[1]);

	fclose(stdin);
	fclose(stdout);

	return 0;
}