Cloudera Hadoop 环境搭建(离线安装)
关于CDH和Cloudera Manager
CDH (Cloudera's Distribution, including Apache Hadoop),是Hadoop众多分支中的一种,由Cloudera维护,基于稳定版本的Apache Hadoop构建,并集成了很多补丁,可直接用于生产环境。
Cloudera Manager则是为了便于在集群中进行Hadoop等大数据处理相关的服务安装和监控管理的组件,对集群中主机、Hadoop、Hive、Spark等服务的安装配置管理做了极大简化。
系统环境
- 实验环境:VMware虚拟机
- 操作系统:CentOS 7 x64
- Cloudera Manager:5.13.0
- CDH: 5.13.0
安装说明
官方共给出了3中安装方式:第一种方法必须要求所有机器都能连网,由于最近各种国外的网站被墙的厉害,我尝试了几次各种超时错误,巨耽误时间不说,一旦失败,重装非常痛苦。第二种方法下载很多包。第三种方法对系统侵入性最小,最大优点可实现全离线安装,而且重装什么的都非常方便。后期的集群统一包升级也非常好。这也是我之所以选择离线安装的原因。
相关包的下载地址
CDH5下载地址:http://archive.cloudera.com/cdh5/parcels/5.13/
Cloudera Manager下载地址:http://archive.cloudera.com/cm5/redhat/7/x86_64/cm/5.13.0/RPMS/x86_64/
准备工作:系统环境搭建
1. 关闭防火墙
systemctl stop firewalld.service #停止firewall
systemctl disable firewalld.service #禁止firewall开机启动
firewall-cmd --state #查看默认防火墙状态
2. 关闭SElinux
l 修改/etc/selinux/config 文件
l 将SELINUX=enforcing改为SELINUX=disabled
l 重启机器即可
3. 各节点可以SSH登陆
ssh-copy-id -i /root/.ssh/id_rsa root@xxx,xxx,xxx,xxx
4. 在修改/etc/hostname主机名称,/etc/hosts中添加各节点的主机名,
5. 设置时间同步
yum -y install ntp ntpdate #安装ntpdate工具
ntpdate cn.pool.ntp.org #设置系统时间与网络时间同步
hwclock --systohc #将系统时间写入硬件时间
安装Cloudrea Manager
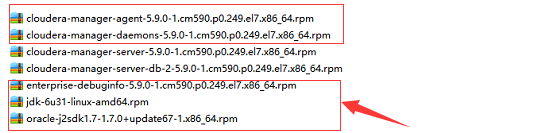
安装rpm文件
l 将下载的rpm包放入文件夹rpm(文件夹名随意)
l cd ./rpm(进入rpm目录)
l yum localinstall –-nogpgcheck *.rpm(安装rpm包)
server节点安装

agent节点安装
启动server节点服务
service cloudera-scm-server start;
配置config.ini文件
修改主机名
修改前为:localhost 修改后为:master

配置本地源
把以下载的.parcel文件,.parcel.sha文件和manifest.json文件拷贝到/opt/cloudera/parcel-repo/文件夹下
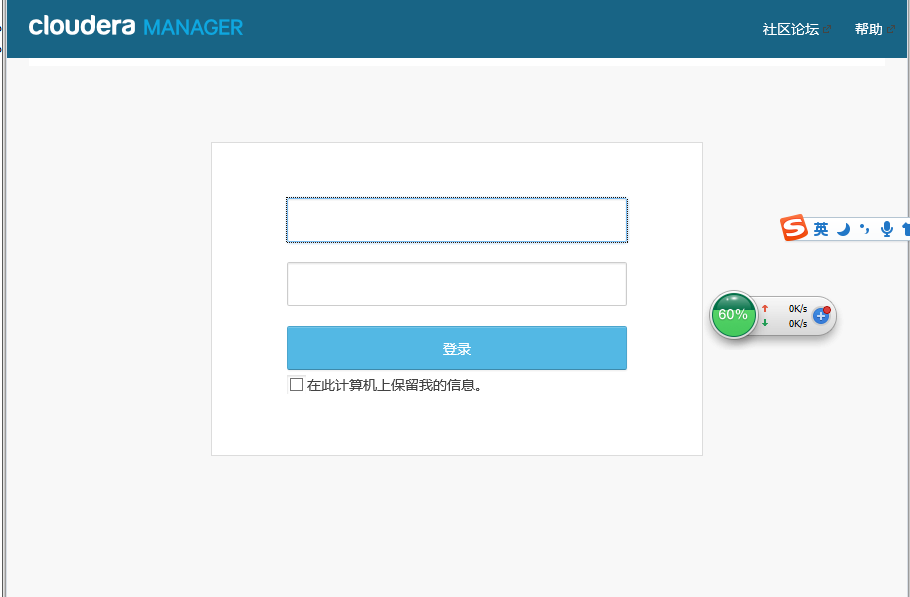
登录CM (账号:admin 密码:admin)
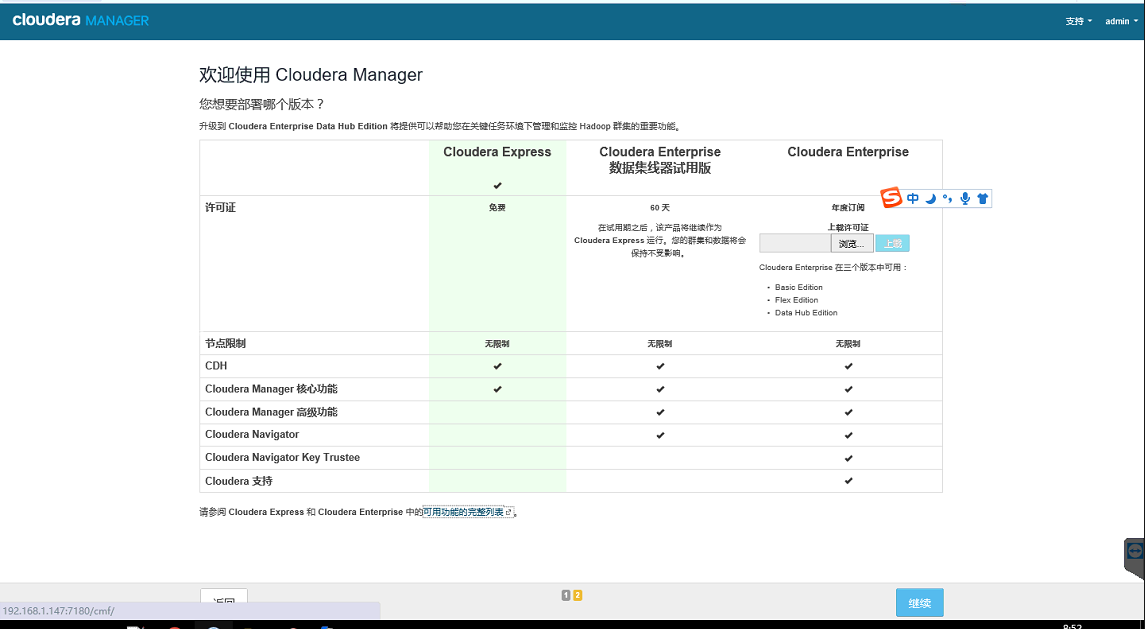
安装集群,包括Hadoop,YARN,Hive等
Hadoop及其组件安装选择Cloudera版本
选中受管理的主机

选择安装方式(Cloudera推荐使用Parcel)
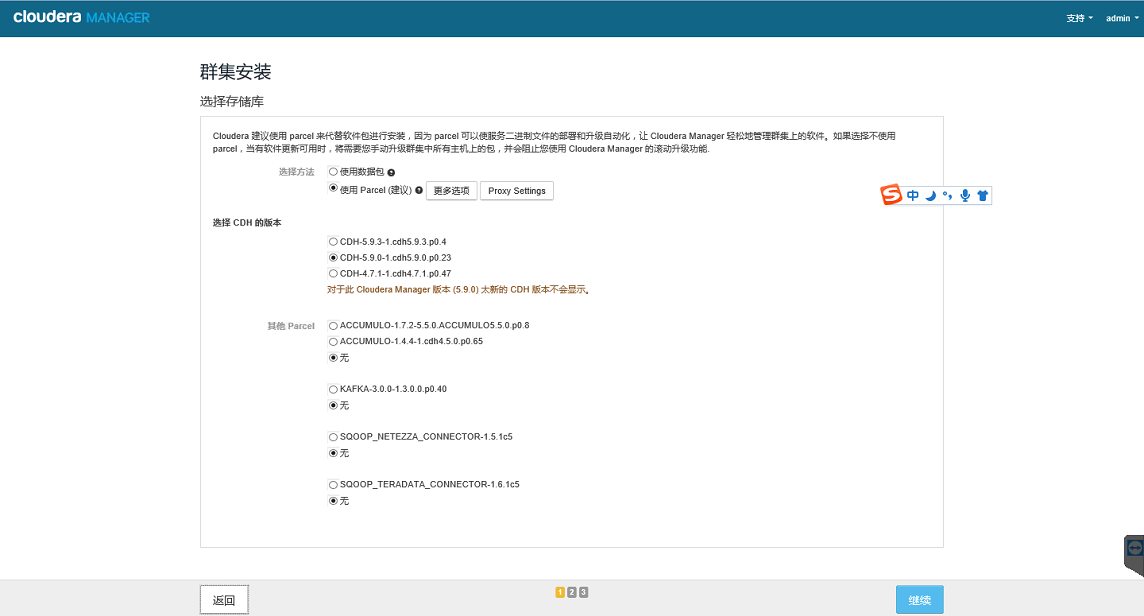
安装选定 Parcel
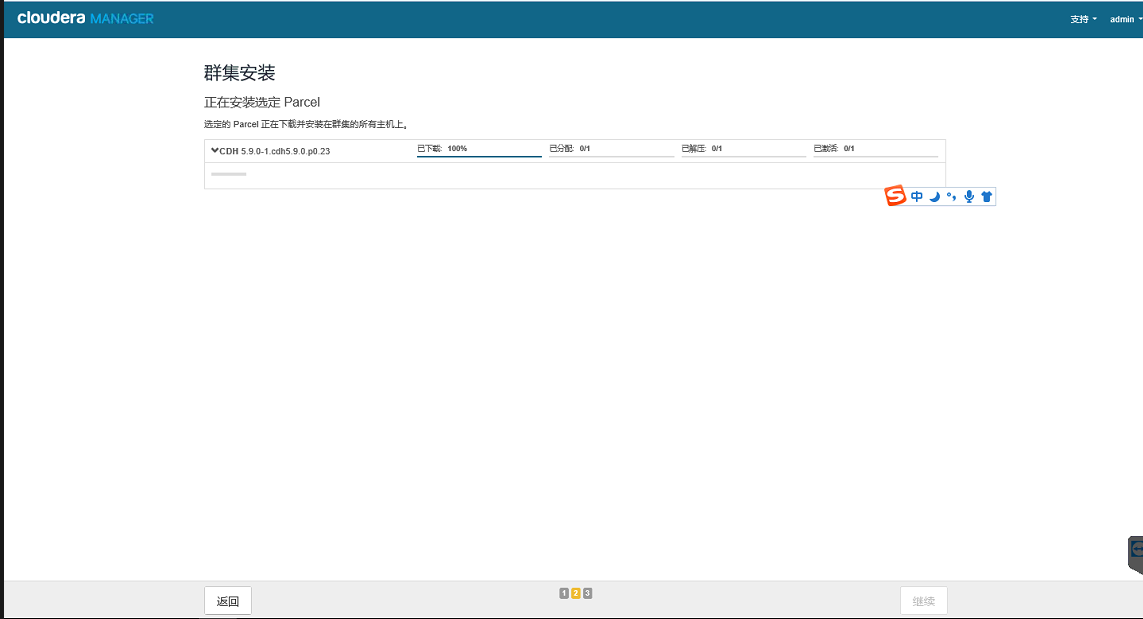
添加服务
服务安装完成
向集群增加节点增加主机
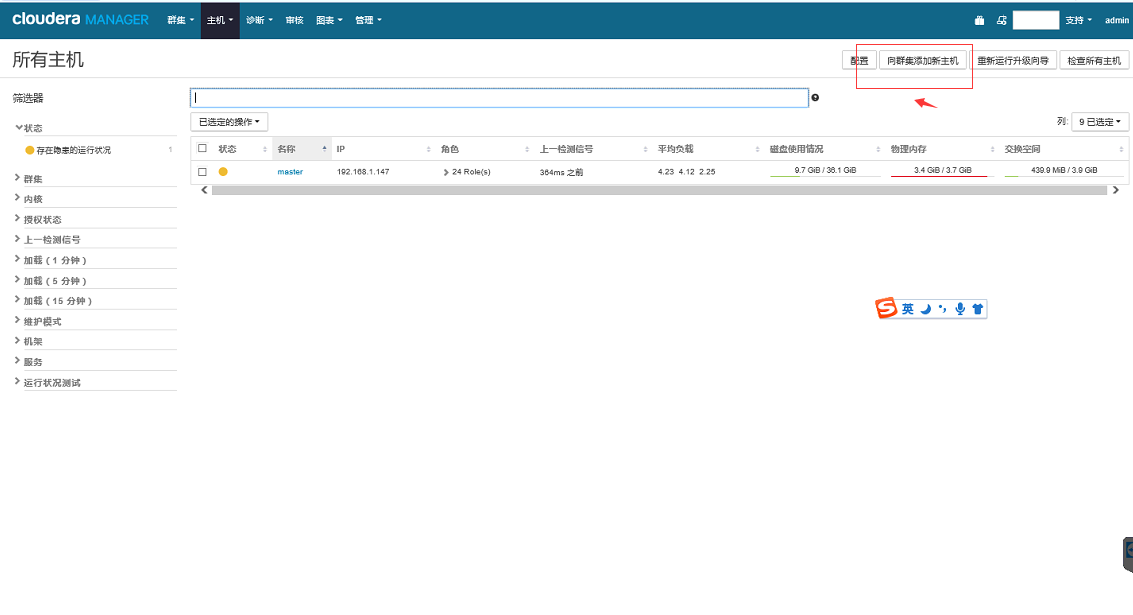
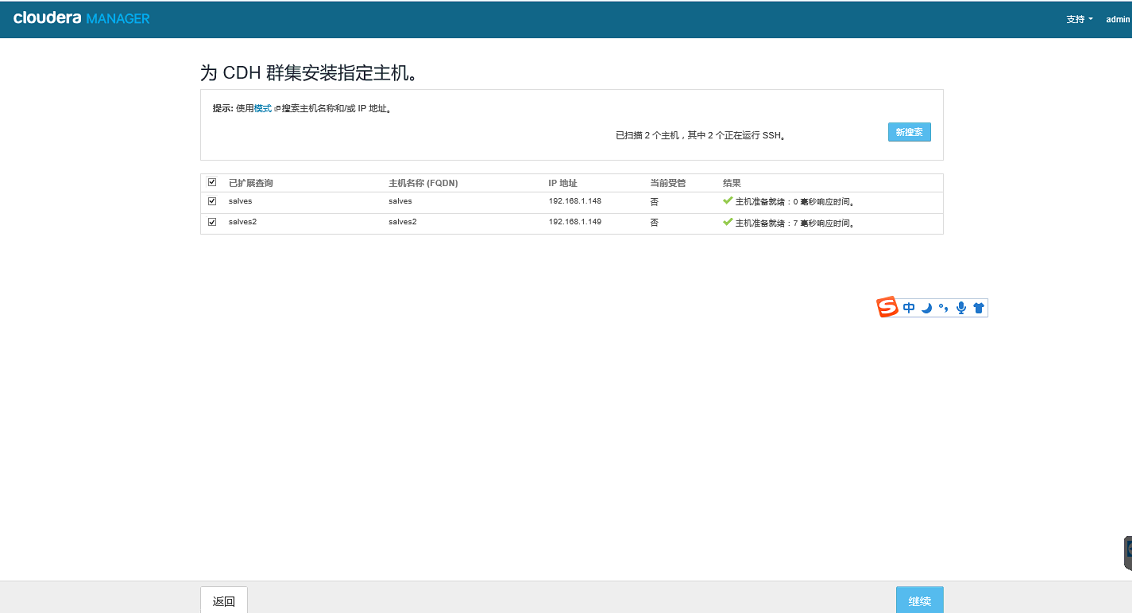
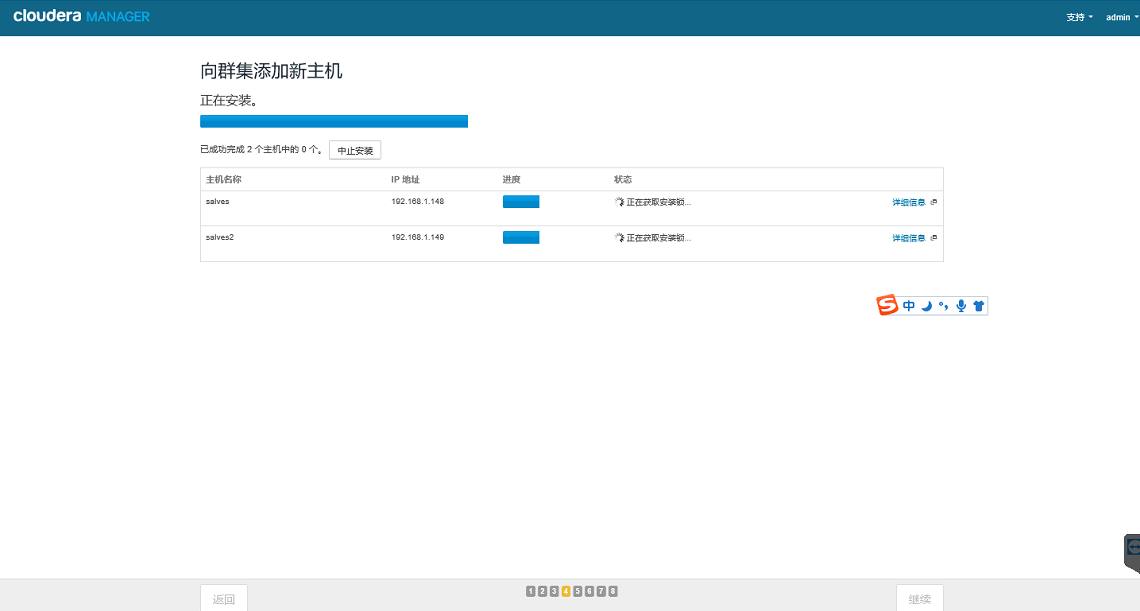
主机添加完成

添加选定 Parcel

验证,安装完成
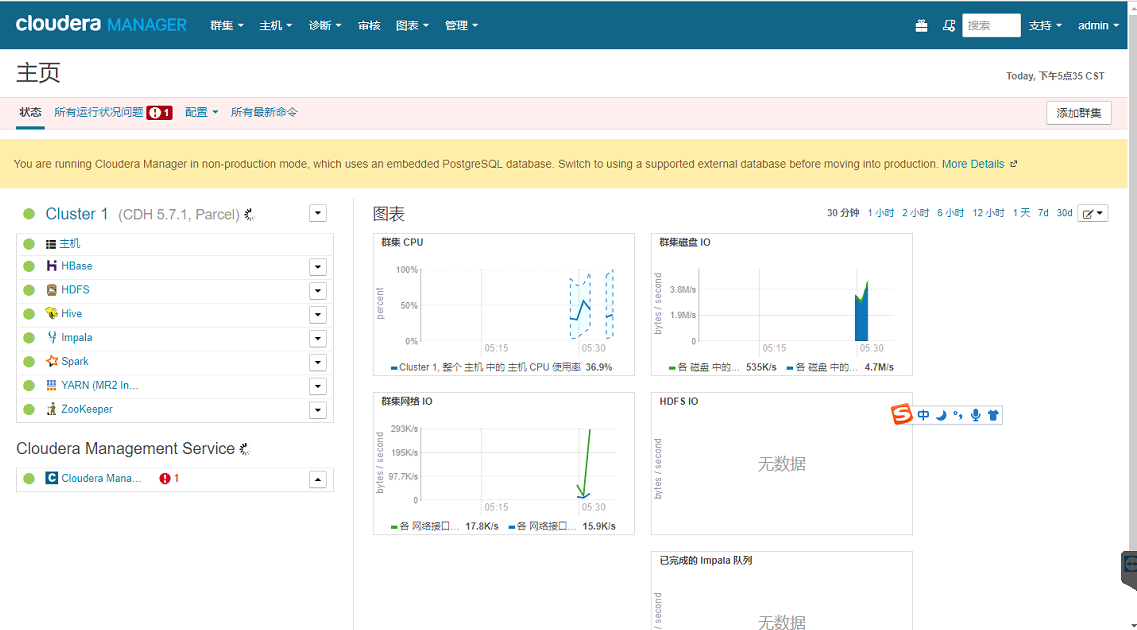
Cloudera Hadoop 环境搭建(离线安装)的更多相关文章
- VS2010+Qt5.4.0 环境搭建(离线安装)
原创作者:http://blog.csdn.net/solomon1558/article/details/44084969 前言 因项目需要Qt开发GUI,我根据网上资料及自己的经验整理了搭建vs2 ...
- Hadoop环境搭建2_hadoop安装和运行环境
1 运行模式: 单机模式(standalone): 单机模式是Hadoop的默认模式.当首次解压Hadoop的源码包时,Hadoop无法了解硬件安装环境,便保守地选择了最小配置.在这种默认模式下所有 ...
- 使用Docker搭建Cloudera Hadoop 环境搭建
单节点 单节点:https://hub.docker.com/r/cloudera/quickstart/ 相关命令 docker pull cloudera/quickstart:latest do ...
- Ubuntu中Hadoop环境搭建
Ubuntu中Hadoop环境搭建 JDK安装 方法一:通过命令行直接安装(不建议) 有两种java可以安装oracle-java8-installer以及openjdk (1)安装oracle-ja ...
- 大数据学习之Hadoop环境搭建
一.Hadoop的优势 1)高可靠性:因为Hadoop假设计算元素和存储会出现故障,因为它维护多个工作数据副本,在出现故障时可以对失败的节点重新分布处理. 2)高扩展性:在集群间分配任务数据,可方便的 ...
- 转 史上最详细的Hadoop环境搭建
GitChat 作者:鸣宇淳 原文:史上最详细的Hadoop环境搭建 关注公众号:GitChat 技术杂谈,一本正经的讲技术 [不要错过文末活动哦] 前言 Hadoop在大数据技术体系中的地位至关重要 ...
- 【转】RHadoop实践系列之一:Hadoop环境搭建
RHadoop实践系列之一:Hadoop环境搭建 RHadoop实践系列文章,包含了R语言与Hadoop结合进行海量数据分析.Hadoop主要用来存储海量数据,R语言完成MapReduce 算法,用来 ...
- eclipse工具下hadoop环境搭建
eclipse工具下hadoop环境搭建: window10操作系统中搭建eclipse64开发系统,配置hadoop的eclipse插件,让eclipse可以查看Hdfs中的文件内容. ...
- Linux集群搭建与Hadoop环境搭建
今天是8月19日,距离开学还有15天,假期作业完成还是遥遥无期,看来开学之前的恶补是躲不过了 今天总结一下在Linux环境下安装Hadoop的过程,首先是对Linux环境的配置,设置主机名称,网络设置 ...
随机推荐
- 1208C Magic Grid
题目大意 给你一个n 让你用0~n^2-1的数填满一个n*n的正方形 满足每个数值出现一次且每行每列的异或值相等 输出任意一种方案 分析 我们发现对于4*4的正方形 0 1 2 3 4 5 ...
- 深入RESTful无状态原则
目录 目录 前言 无状态原则 Web服务的状态 基于状态的Web服务 基于无状态的Web服务 总结两者的区别 前言 在上篇RESTful基础知识中整体的介绍了RESTful架构设计思想的框架,在往后的 ...
- Linux_Bash常用脚本
目录 目录 从用户列表中过滤用户名并创建用户 awktrcut 指令的文本处理 tr指令 cut指令 awk指令 备份文件 测试LFTPServer权限设定 开启Httpd 安装Httpd 批量创建用 ...
- MySQL 基准测试
这是<高性能 MySQL(第三版)>第二章的读书笔记. 基准测试(benchmark)是针对系统的压力测试,用于掌握系统行为或重新系统的某个状态.sysbench 是常用的 MySQL 基 ...
- Maven系列学习(二)Maven使用入门
Maven使用入门 通过上一节的学习,我们已经了解和配置好了Maven,接下来需要编写代码了 1.POM(Project Object Model,项目对象模型) 和Make的Makefile类似,M ...
- phpstudy开启PHPSocket扩展(windows系统)
PHP开启Socket扩展 一.windows系统(本地电脑) 1.打开phpstudy,设置——>配置文件——>打开php.ini(我安装的是PhpStudy v8.0,其他版本请自己找 ...
- angularJS拦截路由
$rootScope.$on('$stateChangeStart', function(event, toState, toParams, fromState, fromParams)
- SpringMVC请求处理流程源码
我们首先引用<Spring in Action>上的一张图来了解Spring MVC 的核心组件和大致处理流程: 从上图中看到①.DispatcherServlet 是SpringMVC ...
- spring-第十七篇之spring AOP基于注解的零配置方式
1.基于注解的零配置方式 Aspect允许使用注解定义切面.切入点和增强处理,spring框架可以识别并根据这些注解来生成AOP代理.spring只是用了和AspectJ 5一样的注解,但并没有使用A ...
- [BZOJ2138]stone(Hall定理,线段树)
Description 话说Nan在海边等人,预计还要等上M分钟.为了打发时间,他玩起了石子.Nan搬来了N堆石子,编号为1到N,每堆 包含Ai颗石子.每1分钟,Nan会在编号在\([L_i,R_i] ...
