BestCoder Round #39 解题报告

　　现场只做出前三题w

　　不过不管怎样这既是第一次认真打BC

　　又是第一次体验用在线编译器调代码

　　订正最后一题花了今天一整个下午（呜呜

　　收获还是比较大的^_^

---

　Delete

wld有n个数(a1,a2,...,an)，他希望进行k次删除一个数的操作，使得最后剩下的n−k个数中有最多的不同的数,保证1≤n≤100,0≤k<n,1≤ai≤n(对于任意1≤i≤n)

　　比较简单的贪心...

　　把出现一次以上的多于一次的部分都删除掉

　　如果k依然>0就要删去k种不同的数

---

Multiple


wld有一个序列a[1..n], 对于每个1≤i<n, 他希望你求出一个最小的j（以后用记号F(i)表示），满足i<j≤n, 使aj为ai的倍数（即aj mod ai＝0），若不存在这样的j，那么此时令F(i) = 0
保证1≤n≤10000,1≤ai≤10000 对于任意 1≤i≤n, 且对于任意1≤i,j≤n(i!=j)，满足ai != aj

　　n^1.5次的大暴力即可

　　发现BC好多题目都是用这种方法...在此之前并不认为这样可以过

　　对于每个数枚举它所有的因数，刷新它们的f[i]值

---

Code


wld有一个长度为n的序列a1..an
wld想要你给出下面这段c++代码的输出：
int calc()
{
	int res=0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			res+=gcd(a[i],a[j])*(gcd(a[i],a[j])-1);
			res%=10007;
		}
	return res;
}
保证1≤n≤10000,1≤ai≤10000 (对于任意1≤i≤n)

　　我的做法是n^1.5次的，但是发现题解是nlog(n)

　　但上次莫比乌斯反演只看到一半...所以先弃疗吧

　　讲讲n^1.5次的做法

　　首先n^1.5的复杂度将每个数的因子打上标记

　　我们可以枚举最大公约数d，如果有x个数有d这个因子

　　那么就累计x*(x-1)次这个答案

　　但是显然我们会发现问题

　　如果两个数有4这个因子，那么在统计2的时候又会统计一次！

　　解决方法很简单，我们可以预先处理出每个数应累计的答案f[i]

　　枚举最大公约数d的同时，再枚举d的因子i，减去这个因子的答案

　　注意：这里的答案也是处理过的答案，即f[i]

　　最后单独累计i=j时的情况

　　

　　手速太慢...原因有好多个

　　开始写的时候把+=看成了*=

　　所以写了乘法逆元...然后调了半天输出了很多中间过程才发现错误

　　然后还忘记了i=j的情况

　　后来WA了一发，是因为枚举最大公约数的时候应枚举到a[i]的最大值而不是n

　　刚开始没查出来，又开始证明算法的思路即f[i]的计算是否正确

　　改来改去越来越离谱..突然发现是后面的问题

　　然后就1h+辣> <

---

Lucky


wld有n个数(a1...an)
保证对于任意1≤i≤n，1≤ai≤n
wld有一个常数k保证2≤k≤2∗n
为了消除歧义保证k为奇数
他有m个询问
每个询问有参数l1,r1,l2,r2
保证(1≤l1≤r1<l2≤r2≤n)
对于每个询问你需要回答有多少个二元组(i，j)满足：
l1≤i≤r1且l2≤j≤r2且ai+aj=k
保证1≤n≤30000,1≤m≤30000

　　

　　恩..这道题在考场上确实是写不出来的..

　　今天下午去学习了一下莫队算法...觉得很有趣...

　　

　　莫队算法就是建立在分块基础上，离线解决一系列区间询问问题

　　首先这道题假设已知[l,r]中相加=k的对数

　　那么我们可以通过复杂度不高的代价得知[l-1,r][l+1,r][l,r-1][l,r+1]的答案

　　刚开始是打算用log级的倍增做的..但是交了一发TLE了

　　这道题询问的是[l1,r1][l2,r2]中满足条件的对数

　　如何转换成单个区间上面[l,r]中相加=k的对数呢

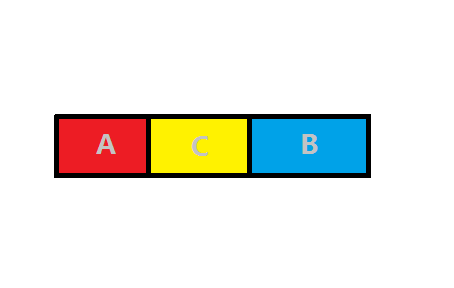
　　假设题目中让我们求的是一个在区间A，一个在区间B的答案，我们假设为F(A,B),并且令F中统计的数对为有序的

　　即只统计a[i]+a[j]=k且(i<j)的情况

　　可以证明得出F(A,B) = F(A+C+B,A+C+B)-F(A+C,A+C)-F(B+C,B+C)+F(C,C)

　　F(A+C+B,A+C+B)-F(A+C,A+C)-F（C+B,C+B)+F（C,C）

　　= F(A,A)+F(A,C)+F(A,B)+F(C,C)+F(C,B)+F(B,B)-F(A,A)-F(A,C)-F(C,C)-F(C,C)-F(C,B)-F(B,B)+F(C,C)

　　= F(A,B)

　　转化成了4部分两区间相等的F，也就是可以用上面的莫队算法来解决了

　　最后一个问题，就是转移的时候如何从log(n)转化成O（1）

　　在执行莫队的同时，即l,r一位一位移动的时候，用一个数组记录当前区间内某个数出现的次数就可以了...

　　

---

　　涨了177w

　　手速还是慢慢慢

　　居然过了一个周末一下子就27号了呢

　　居然再过两天又要回家了呢

　　

　　27/.Apr.