洛谷P1829 [国家集训队]Crash的数字表格 / JZPTAB(莫比乌斯反演)

题目背景

提示：原 P1829 半数集问题已经迁移至 P1028 数的计算

题目描述

今天的数学课上，Crash小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数a和b，LCM(a, b)表示能同时整除a和b的最小正整数。例如，LCM(6, 8) = 24。

回到家后，Crash还在想着课上学的东西，为了研究最小公倍数，他画了一张N*M的表格。每个格子里写了一个数字，其中第i行第j列的那个格子里写着数为LCM(i, j)。一个4*5的表格如下：

1    2    3    4    5

2    2    6    4    10

3    6    3    12    15

4    4    12    4    20

看着这个表格，Crash想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题：这个表格中所有数的和是多少。当N和M很大时，Crash就束手无策了，因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大，Crash只想知道表格里所有数的和mod20101009的值。

输入输出格式

输入格式：

输入的第一行包含两个正整数，分别表示N和M。

输出格式：

输出一个正整数，表示表格中所有数的和mod20101009的值。

输入输出样例

输入样例#1：复制

4 5

输出样例#1：复制

说明

30%的数据满足N, M≤ 10^3。

70%的数据满足N, M≤ 10^5。

100%的数据满足N, M≤ 10^7。

Orz gxz

https://www.cnblogs.com/GXZlegend/p/6999816.html

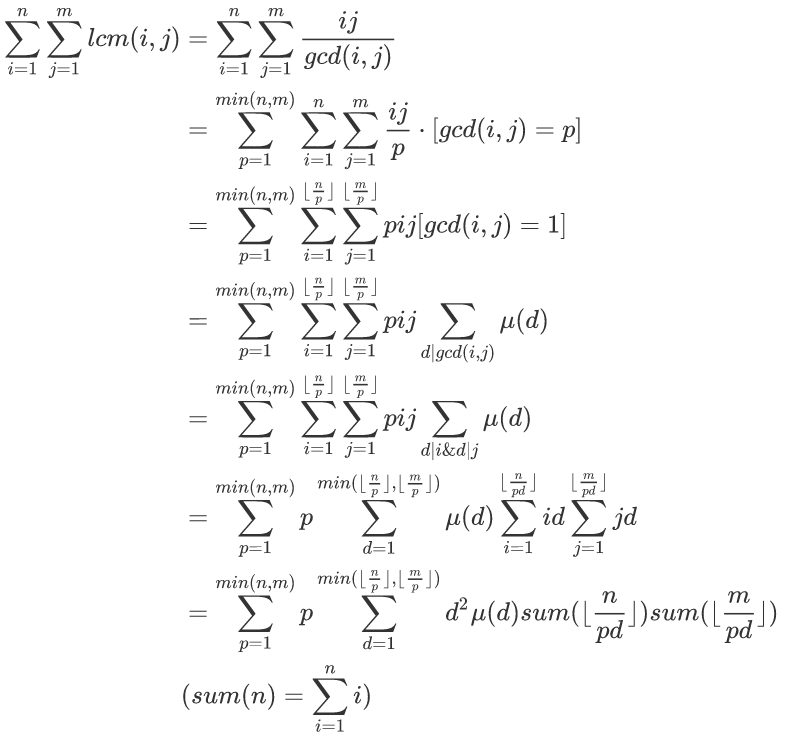
然后分块套分块

时间复杂度$O(n)$

// luogu-judger-enable-o2

#include<cstdio>

#include<algorithm>

#define LL long long

using namespace std;

const int MAXN = 1e7 + , mod = ;

int N, M;

int prime[MAXN], tot, mu[MAXN], vis[MAXN];

LL sum[MAXN];

void GetMu(int N) {

    mu[] = ; sum[] = ;

    for(int i = ; i <= N; i++) {

        if(!vis[i]) mu[i] = -, prime[++tot] = i;

        for(int j = ; j <= tot && i * prime[j] <= N; j++) {

            vis[i * prime[j]] = ;

            if(!(i % prime[j])) {mu[i * prime[j]] = ; break;}

            else mu[i * prime[j]] = -mu[i];

        }

    }

    for(LL i = ; i <= N; i++) sum[i] = (1ll * i * i % mod * mu[i] % mod + sum[i - ] + mod) % mod;

}

LL S(LL x) {

    return 1ll * (x + ) * x /  % mod;//interesting

}

LL Query(int n, int m) {

    int last = ;LL ret = ;

    for(int d = ; d <= n; d = last + ) {

        last = min(n / (n / d), m / (m / d));

        ret = (ret + 1ll * (sum[last] - sum[d - ] + mod) % mod * S(n / d) % mod * S(m / d) % mod) % mod;

    }

    return ret % mod;

}

int main() {

//    freopen("nt2011_table.in", "r", stdin);

//    freopen("nt2011_table.out", "w", stdout);

    scanf("%d %d", &N, &M);

    if(N > M) swap(N, M);

    GetMu(1e7 + );

    int last = ; LL ans = ;

    for(int p = ; p <= N; p = last + ) {

        last = min(N / (N / p), M / (M / p));

        ans = (ans + 1ll * (S(last) - S(p - ) + mod) % mod * (Query(N / p, M / p)) % mod) % mod;

    }

    printf("%lld", ans % mod);

    return ;

}

/*

123 321

*/