高斯消元法的C++简单实现

高斯消元法

　　首先，我们导入几个概念。

定义1： 一个矩阵称为阶梯形（行阶梯形），若它有以下三个性质：

　　1.每一非零行在每一零行之上；

　　2.某一行的先导元素所在的列位于前一行先导元素的后面；

　　3.某一行先导元素所在列下方元素都是零。

　　比如，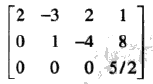

定义2：若一个阶梯形矩阵还满足以下性质，称它为简化阶梯形（简化行阶梯形）：

　　1.每一非零行的先导元素是1；

　　2.每一先导元素1是该元素所在列的惟一非零元素。

　　比如，

定理1：每个矩阵行等价于惟一的简化阶梯形矩阵。即简化阶梯形矩阵是惟一的。

---

　　下面，我们用一个具体例子来说明高斯消元法的主要步骤。

　　原矩阵：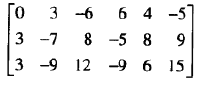

　　第一步，由最左的非零列开始，这是一个主元列。主元位置在该列顶端。

　　第二步，在主元列中选取一个非零元作为主元。若有必要的话，对换两行使这个元素移到主元位置上。

　　第三步，用倍加行变换将主元下面的元素变成0.

　　第四步，暂时不管包含主元位置的行以及它上面的各行，对剩下的子矩阵使用上述的三个步骤直到没有非零行需要处理为止。

　　对每一行重复上述步骤。

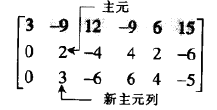
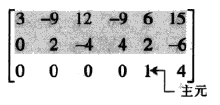
　　第五步，由最右面的主元开始，把每个主元上方的各元素变成0.若某个主元不是1，用倍乘变换将它变成1.

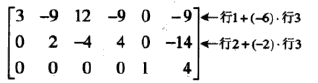
　　最后，我们就得到了原矩阵的简化阶梯形。

　　其中，第1~4步称为行化简算法的向前步骤，产生唯一的简化阶梯形的第5步，称为向后步骤。

---

C++实现

　　我们尝试用C++来实现以上步骤。这里只是简单的实现，也就是用代码描述了上述步骤，没有考虑过多的问题。欢迎大家在评论里指出问题，提出更好的建议，以便于日后改进。

　　大概的实现思路就是先实现向前步骤：

　　首先，我们对于每一行找到第一个不为零的元素，并且将这一行置为1 * * * *的形式，用这一行乘上倍数加到之后的每一行。

　　再实现向后步骤：

　　然后，我们从最后一行开始，选择主元，加到之前的每一行上，使得该列的元素都为零。

　　最后，我们就完成了化简，得到了简化阶梯形。

　　以上算法只是一个粗略实现，主要体现在：

　　1.对于主元的选定不够最优；

　　2.会出现精度问题；

　　3.对于某些情况无法处理。

　　先暂时贴上代码，之后有时间再进行优化。

 #include <iostream>
 #include <cstdio>

 using namespace std;

 int main()
 {
     double martix[][];
     int n, m; // n行m列

     scanf("%d %d", &n, &m);

     // 输入
     for(int i = ; i < n; i++)
         for(int j = ; j < m; j++)
             scanf("%lf", &martix[i][j]);

     // 向前步骤
     for(int i = ; i < n - ; i++)
     {
         // 找主元
         int pos = ;
         for(int j = ; j < m; j++)
             if(martix[i][j])
             {
                 pos = j;
                 break;
             }

         if(martix[i][pos] !=  && martix[i][pos] != )
         {
             double tmp = martix[i][pos];
             for(int j = pos; j < m; j++)
             {
                 martix[i][j] = martix[i][j] / tmp;
             }
         }
         for(int j = i + ; j < n; j++)
         {
             if(!martix[j][pos])
                 continue;
             double tmp = martix[j][pos];
             for(int k = pos; k < m; k++)
             {
                 martix[j][k] = martix[j][k] - martix[i][k] * tmp;
             }
         }
     }

     // 向后步骤
     for(int i = n - ; i > ; i--)
     {
         int pos = ;
         for(int j = ; j < m; j++)
             if(martix[i][j])
             {
                 pos = j;
                 break;
             }

         if(martix[i][pos] !=  && martix[i][pos] != )
         {
             double tmp = martix[i][pos];
             for(int j = pos; j < m; j++)
             {
                 martix[i][j] = martix[i][j] / tmp;
             }
         }

         for(int j = ; j < i; j++)
         {
             if(!martix[j][pos])
                 continue;
             double tmp = martix[j][pos];
             for(int k = pos; k < m; k++)
             {
                 martix[j][k] = martix[j][k] - martix[i][k] * tmp;
             }
         }
     }

     // 输出
     for(int i = ; i < n; i++)
     {
         for(int j = ; j < m; j++)
             printf("%-10.2f", martix[i][j]);
         printf("\n");
     }
     return ;
 }