[ZJOI2015]幻想乡战略游戏（点分树）

题意自己看。。。

思路

没想到今（昨）天刷着刷着点分治的水题，就刷出来了一个点分树。。。

然后就疯狂地找题解，代码，最后终于把它给弄懂了。

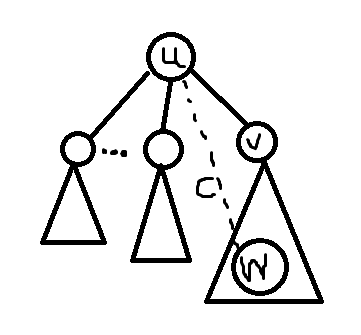
点分树——动态点分治，对于此题来说，我们设u为当前的补给站位置，v是它的一个儿子。同时设dis(i,j)为树上i点到j点的距离。cnt_i为以i为根的子树中d（也就是军队数）的总量

我们把补给站从u转移到v（假设u是树的根），答案的变化为dis(u,v)*(cnt_u-cnt_v)-dis(u,v)*cnt_v=dis(u,v)*(cnt_u-2*cnt_v)

所以当2*cnt_v>cnt_u把补给站转移v会使答案变优，一直这样操作下去，直到不管如何转移都无法使答案变优，当前点就是答案。

我们对于每一次修改都维护一下然后默认当前点为补给站且为当前树的根，然后像刚才一样转移补给站，就有了这个题的大体思路。

但这样肯定会爆炸啊（每次只会转移一步，复杂度和深度有关）

所以我们就可以用到点分树了。

我们利用点分治的方法（找重心作为根节点，然后递归处理子树）重新构建一颗树，称为分治树。

举个例子，比如说样例

（左为原树右为分治树）

这样我们就得到一颗深度为log的树。

这样我们转移就不会因为深度太大而GG了。

但是，这样一来的话因为树的结构不一样了，补给站的转移就会很难。因为一个点在分治树的儿子在原树中不一定和它直接相连

（之后我们的补给站的转移都是在分治树上进行的）

但还是有办法解决的。我们记录这这些东西。dis(i,j)为i,j在原树的距离。cnt[i]为分治树中以i为根的子树中有多少个d，sum_i为分治树中以i为根的子树中所有的点j的dis(i,j)*dj之和，sumch_(i,j)记录i点第j个儿子的sum。

我们现在讨论从u转移到它分治树中的一个子节点v，v是原来这颗子树中的重心但在原树中并不一定和u之间相连，我们设原树中直接和u相连的点是w。

因为把补给站转到v的时候要把v作为整棵树的根，只要把v所在子树之外的所有信息扔到w中然后递归就可以了。那怎么维护w的信息呢？

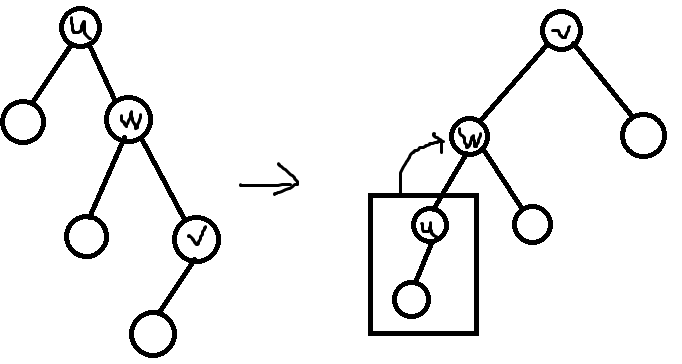
我们记录在v处记录下w和w与u这条边的权值c，然后我们在cnt_w处加上cnt[u]-cnt[v],然后在sum_w处加上sum[u]-sumch_(i,v)+(cnt[u]-cnt[v])*c;

最后答案就取sum[当前点]就行了。

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 #include<vector>
 using namespace std;
 #define int long long
 const int N=1e5+;
 struct son{int v,rv,w;};
 struct node{int u,c,w;};
 struct pre{int to,w;};
 vector<son>ch[N];
 vector<node>stack;
 vector<pre>f[N];
 vector<int>sumch[N];
 int num,head[N];
 int g[N],root,size[N],all,vis[N];
 int realroot,sum[N],cnt[N],n,m;
 struct edge{
     int to,nxt,w;
 }e[N*];
 void add_edge(int u,int v,int w){
     num++;
     e[num].nxt=head[u];
     e[num].to=v;
     e[num].w=w;
     head[u]=num;
 }
 int read(){
     int sum=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){sum=sum*+ch-'';ch=getchar();}
     return sum*f;
 }
 void getroot(int u,int f){
     g[u]=;size[u]=;
     for(int i=head[u];i;i=e[i].nxt){
         int v=e[i].to;
         if(v==f||vis[v])continue;
         getroot(v,u);
         g[u]=max(g[u],size[v]);
         size[u]+=size[v];
     }
     g[u]=max(g[u],all-size[u]);
     if(g[u]<g[root])root=u;
 }
 void dfs(int u,int fa,int top,int w){
     pre x;x.to=top;x.w=w;
     f[u].push_back(x);
     size[u]=;
     for(int i=head[u];i;i=e[i].nxt){
         int v=e[i].to;
         if(vis[v]||v==fa)continue;
         dfs(v,u,top,w+e[i].w);
         size[u]+=size[v];
     }
 }
 void work(int u){
     pre y;y.w=;y.to=u;
     f[u].push_back(y);
     vis[u]=;
     for(int i=head[u];i;i=e[i].nxt){
         int v=e[i].to;
         if(vis[v]==)continue;
         dfs(v,,u,e[i].w);
         root=,all=size[v];
         getroot(v,);
         son x;x.v=root;x.rv=v;x.w=e[i].w;
         ch[u].push_back(x);
         work(root);
     }
 }
 void update(int u,int c,int w){
     for(int i=;i<f[u].size();i++){
         int v=f[u][i].to;
         int L=f[u][i].w;
         cnt[v]+=c;
         sum[v]+=w+c*L;
         if(i!=f[u].size()-)
             for(int j=;j<ch[v].size();j++){
                 if(ch[v][j].v==f[u][i+].to)sumch[v][j]+=w+c*L;
             }
     }
 }
 int check(){
     int now=realroot,mx;
     stack.clear();
     while(now){
         mx=;
         for(int i=;i<ch[now].size();i++)
             if(cnt[ch[now][i].v]>cnt[ch[now][mx].v])mx=i;
         if(ch[now].size()==||cnt[ch[now][mx].v]*<=cnt[now]){
             int ans=sum[now];
             for(int i=;i<stack.size();i++)
                 update(stack[i].u,stack[i].c,stack[i].w);
             return ans;
         }
         int v=ch[now][mx].v;
         node x;
         x.u=ch[now][mx].rv;x.c=-(cnt[now]-cnt[v]);
         x.w=-(sum[now]-sumch[now][mx]+(cnt[now]-cnt[v])*ch[now][mx].w);
         stack.push_back(x);
         update(x.u,-x.c,-x.w);
         now=v;
     }
 }
 signed main(){
     n=read();m=read();
     for(int i=;i<n;i++){
         int u=read(),v=read(),w=read();
         add_edge(u,v,w);add_edge(v,u,w);
     }
     g[]=n+;root=;all=n;
     getroot(,);realroot=root;
     work(root);
     for(int i=;i<=n;i++)sumch[i]=vector<int>(ch[i].size(),);
     while(m--){
         int x=read(),y=read();
         update(x,y,);
         printf("%lld\n",check());
     }
     return ;
 }