[JLOI2011]飞行路线（分层图）

[JLOI2011]飞行路线

题目描述

Alice和Bob现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在 n 个城市设有业务，设这些城市分别标记为 0 到 n−1 ，一共有 m 种航线，每种航线连接两个城市，并且航线有一定的价格。

Alice和Bob现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多 k 种航线上搭乘飞机。那么Alice和Bob这次出行最少花费多少？

输入输出格式

输入格式：

数据的第一行有三个整数， n,m,k ，分别表示城市数，航线数和免费乘坐次数。

第二行有两个整数， s,t ，分别表示他们出行的起点城市编号和终点城市编号。

接下来有m行，每行三个整数， a,b,c ，表示存在一种航线，能从城市 a 到达城市 b ，或从城市 b 到达城市 a ，价格为 c 。

输出格式：

只有一行，包含一个整数，为最少花费。

输入输出样例

输入样例#1： 复制

5 6 1

0 4

0 1 5

1 2 5

2 3 5

3 4 5

2 3 3

0 2 100

输出样例#1： 复制

8

说明

对于30%的数据, \(2 \le n \le 50,1 \le m \le 300, k =0\)

对于50%的数据, \(2\le n \le 600,1 \le m \le 6000, k \le 1\)

对于100%的数据, \(2\le n \le 10000,1 \le m \le 50000,0 \le k \le 10 \le s,t<n,0 \le a,b<n,a\neq b,0 \le c \le 1000\)

---

题解

分层图的模板题吧。

可以说模板到不能再模板了，比那个集训队论文的题目还要简单。

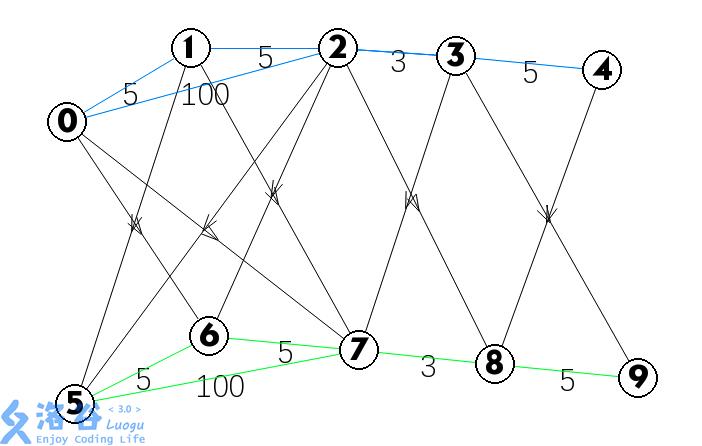
从洛谷偷一张图更直观。

免费的路径就直接接到下一层图吧，然后是不需要消费的。

同一层的路径该消费的还是要消费的，因为只有k层，所以一定不会超出限制哦~.

---

代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
const int N=1e6+5;
struct node{
    int nex,to,v;
}e[N<<2];
int dis[N],vis[N];
int n,m,k,num,head[N];
int s,t;
priority_queue<pair<int,int> >q;
int read(){
    int x=0,w=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*w;
}

void add(int from,int to,int v){
    num++;
    e[num].to=to;
    e[num].v=v;
    e[num].nex=head[from];
    head[from]=num;
}

void dijkstra(){
    memset(dis,63,sizeof(dis));dis[s]=0;
    q.push(make_pair(dis[s],s));
    while(q.size()){
        int u=q.top().second;q.pop();if(vis[u])continue;vis[u]=1;
        for(int i=head[u];i;i=e[i].nex){
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].v){
                dis[v]=dis[u]+e[i].v;
                q.push(make_pair(-dis[v],v));
            }
        }
    }
}

int main(){
    n=read();m=read();k=read();
    if(k>=m){printf("0");return 0;}
    s=read();t=read();t=n*k+t;
    for(int i=1;i<=m;i++){
        int x=read(),y=read(),z=read();
        add(x,y,z);add(y,x,z);
        for(int j=1;j<=k;j++){
            add(x+(j-1)*n,y+j*n,0);
            add(y+(j-1)*n,x+j*n,0);
            add(x+j*n,y+j*n,z);
            add(y+j*n,x+j*n,z);
        }
    }
    dijkstra();
    printf("%d",dis[t]);
    return 0;
}