UVA1583-Digit Generator（紫书例题3.5）

For a positive integer N , the digit-sum of N is defined as the sum of N itself and its digits. When M is the digitsum of N , we call N a generator of M .

For example, the digit-sum of 245 is 256 (= 245 + 2 + 4 + 5). Therefore, 245 is a generator of 256.

Not surprisingly, some numbers do not have any generators and some numbers have more than one generator. For example, the generators of 216 are 198 and 207.

You are to write a program to find the smallest generator of the given integer.

Input

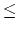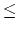Your program is to read from standard input. The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case takes one line containing an integer N , 1N100, 000 .

Output

Your program is to write to standard output. Print exactly one line for each test case. The line is to contain a generator of N for each test case. If N has multiple generators, print the smallest. If N does not have any generators, print 0.

The following shows sample input and output for three test cases.

Sample Input

3
216
121
2005

Sample Output

198
0
1979

思路：此题先打表，然后再查询即可，一次性枚举1到10000，其中a【i】的值是i的最小生成元

#include<iostream>
#include<algorithm>
#include<string>
#include<cmath>
#include<cstdio>
#include<cstring>
using namespace std;
#define maxn 100005       //不妨将数组开大点
int a[maxn];
int main()
{
		memset(a,0,sizeof(a));
		for(int i=1;i<maxn;i++)
		{
			int m=i,n=i;
			while(n)
			{
				m+=n%10;
				n/=10;
			}
			if(a[m]==0||i<a[m])
				a[m]=i;
		}
	int t,n;
	cin>>t;
	while(t--)
	{
		cin>>n;
		cout<<a[n]<<endl;
	}
	return 0;
}