Sampling
本文主要涉及接受拒绝采样,重要性采样,蒙特卡洛方法,吉布斯采样等内容。部分内容整理与互联网。仅供交流学习使用!
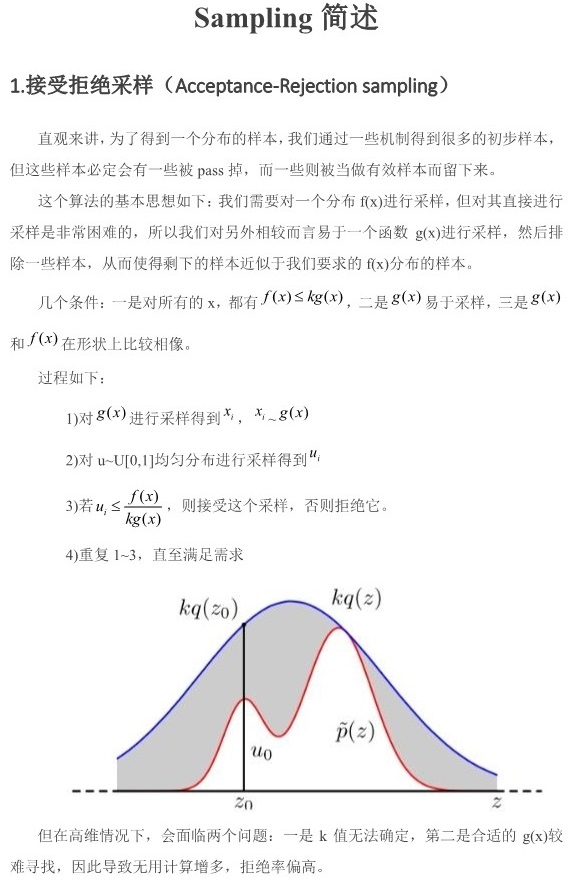





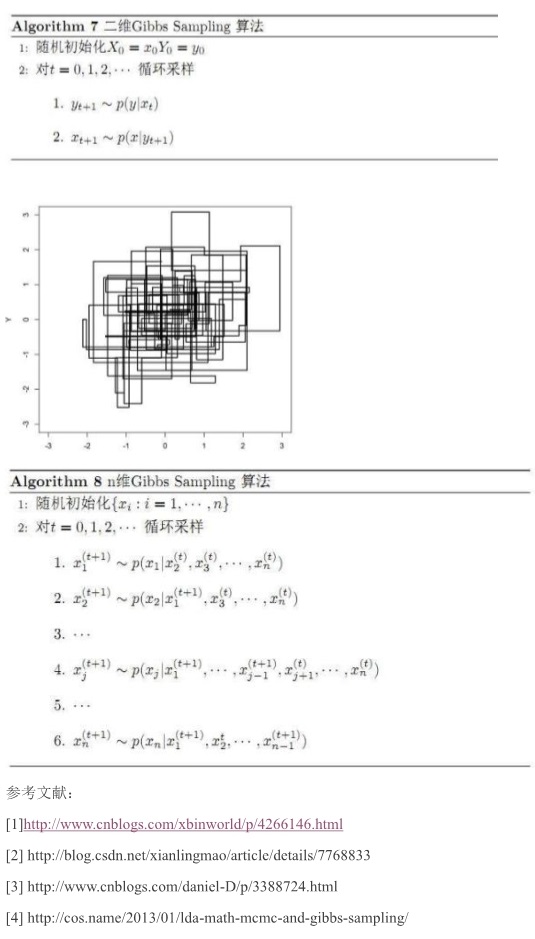

Sampling的更多相关文章
- 图像抠图算法学习 - Shared Sampling for Real-Time Alpha Matting
一.序言 陆陆续续的如果累计起来,我估计至少有二十来位左右的朋友加我QQ,向我咨询有关抠图方面的算法,可惜的是,我对这方面之前一直是没有研究过的.除了利用和Photoshop中的魔棒一样的技术或者 ...
- 【转载】Recommendations with Thompson Sampling (Part II)
[原文链接:http://engineering.richrelevance.com/recommendations-thompson-sampling/.] [本文链接:http://www.cnb ...
- PRML读书会第十一章 Sampling Methods(MCMC, Markov Chain Monte Carlo,细致平稳条件,Metropolis-Hastings,Gibbs Sampling,Slice Sampling,Hamiltonian MCMC)
主讲人 网络上的尼采 (新浪微博: @Nietzsche_复杂网络机器学习) 网络上的尼采(813394698) 9:05:00 今天的主要内容:Markov Chain Monte Carlo,M ...
- 算法系列:Reservoir Sampling
copyright © 1900-2016, NORYES, All Rights Reserved. http://www.cnblogs.com/noryes/ 欢迎转载,请保留此版权声明. -- ...
- 随机采样方法整理与讲解(MCMC、Gibbs Sampling等)
本文是对参考资料中多篇关于sampling的内容进行总结+搬运,方便以后自己翻阅.其实参考资料中的资料写的比我好,大家可以看一下!好东西多分享!PRML的第11章也是sampling,有时间后面写到P ...
- LDA-math-MCMC 和 Gibbs Sampling
http://cos.name/2013/01/lda-math-mcmc-and-gibbs-sampling/ 3.1 随机模拟 随机模拟(或者统计模拟)方法有一个很酷的别名是蒙特卡罗方法(Mon ...
- 蒙特卡洛法计算定积分—Importance Sampling
如上图所示,计算区间[a b]上f(x)的积分即求曲线与X轴围成红色区域的面积.下面使用蒙特卡洛法计算区间[2 3]上的定积分:∫(x2+4*x*sin(x))dx # -*- coding: u ...
- 蓄水池采样算法(Reservoir Sampling)
蓄水池采样算法 问题描述分析 采样问题经常会被遇到,比如: 从 100000 份调查报告中抽取 1000 份进行统计. 从一本很厚的电话簿中抽取 1000 人进行姓氏统计. 从 Google 搜索 & ...
- Reservoir Sampling - 蓄水池抽样
问题起源于编程珠玑Column 12中的题目10,其描述如下: How could you select one of n objects at random, where you see the o ...
- [大牛翻译系列]Hadoop(7)MapReduce:抽样(Sampling)
4.3 抽样(Sampling) 用基于MapReduce的程序来处理TB级的数据集,要花费的时间可能是数以小时计.仅仅是优化代码是很难达到良好的效果. 在开发和调试代码的时候,没有必要处理整个数据集 ...
随机推荐
- 四、Spring Boot 多数据源 自动切换
实现案例场景: 某系统除了需要从自己的主要数据库上读取和管理数据外,还有一部分业务涉及到其他多个数据库,要求可以在任何方法上可以灵活指定具体要操作的数据库.为了在开发中以最简单的方法使用,本文基于注解 ...
- 自学Zabbix3.7-事件Event
配置item.trigger.都是为发送报警做准备的,什么是事件通知呢?简单的说故障发生了,zabbix会发邮件或者短信给你,告诉你服务器的一些状况. 1. 通知条件 发送通知,需要有如下步骤 定义一 ...
- ZKWeb网页框架2.0正式发布
2.0.0更新的内容有 更新框架要求 框架要求从 netstandard 1.6 升到 netstandard 2.0 框架要求从 netcoreapp1.1 升到 netcoreapp2.0 更新引 ...
- 【深度学习系列】用PaddlePaddle和Tensorflow实现GoogLeNet InceptionV2/V3/V4
上一篇文章我们引出了GoogLeNet InceptionV1的网络结构,这篇文章中我们会详细讲到Inception V2/V3/V4的发展历程以及它们的网络结构和亮点. GoogLeNet Ince ...
- acffo的开源项目汇总
1. XWaveView, 流动波浪效果 2.LogRecordHelper, logcat日志记录存储到文件 可以指定TAG , 将logcat日志写入文件 ...
- 【java】实现Interface java.lang.Comparable<T>接口的int compareTo(T o)方法实现对象数组或链表或集合的排序,和挽救式对象比较器Interface java.util.Comparator<T>
package 对象比较排序; import java.util.Arrays; class A implements Comparable<A>{ private String name ...
- JavaScript的setter与getter方法
作者:http://hawkzz.com 以前在写项目过程一直都没有使用过Javascript的setter与getter方法,所以对其是一种要懂不懂的概念:今天看书看到这个知识点,还是模模糊糊的,于 ...
- 数据库入门(以MySQL为例)
一.数据库中的概念 1.数据库是用户存放数据.访问数据.操作数据的存储仓库,用户的各种数据被有组织地存放在数据库中.可以随时被有权限的用户查询.统计.添加.删除.和修改.可以说,数据库是长期存储在计算 ...
- HttpClient4.5 post请求xml到服务器
1.加入HttpClient4.5和junit依赖包 <dependencies> <dependency> <groupId>org.apache.httpcom ...
- open-falcon(v0.2)安装grafana部署
下载rpm wget https://s3-us-west-2.amazonaws.com/grafana-releases/release/grafana-4.4.3-1.x86_64.rpm 本地 ...
