怎么理解超几何分布概率公式:p=C(M,k)C(N-M,n-k)/C(N,n)
怎么理解超几何分布概率公式:p=C(M,k)C(N-M,n-k)/C(N,n)
前言:重在记录,可能出错。
超几何分布概率公式:p=C(M,k)C(N-M,n-k)/C(N,n),也就是: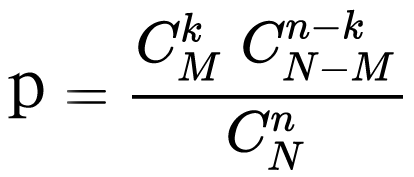
到底要怎么理解呢?
举个例子:
设有N件产品,其中有M件次品,现在从中任取n件,问其中恰有k(k≤M)件次品的概率是多少?
思考:
设N件产品中任取n件为事件A,则事件A共包含 个基本事件。
个基本事件。
设恰好取出k个次品为事件B,此k个次品共有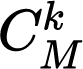 种取法,也就是在M个次品中取k个。接下来,每一种取法对应着需要取出n-k个正品,同理在N-M个正品中取n-k个,有
种取法,也就是在M个次品中取k个。接下来,每一种取法对应着需要取出n-k个正品,同理在N-M个正品中取n-k个,有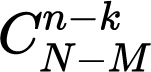 种取法。
种取法。
因此事件B共包含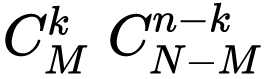 个基本事件。
个基本事件。
根据古典概型的计算方法:P(B)=B事件包含的基本事件数/样本空间中基本事件的总数,因此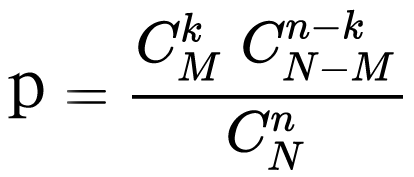
怎么理解超几何分布概率公式:p=C(M,k)C(N-M,n-k)/C(N,n)的更多相关文章
- uva-11021-全概率公式
https://vjudge.net/problem/UVA-11021 有n个球,每只的存活期都是1天,他死之后有pi的概率产生i个球(0<=i<n),一开始有k个球,问m天之后所有球都 ...
- hdu 4762 Cut the Cake概率公式
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4762 题目大意:一个圆形蛋糕,现在要分成M个相同的扇形,有n个草莓,求n个草莓都在同一个扇形上的概率. ...
- HDU 4326Game(比较难理解的概率dp)
Game Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total Subm ...
- Chapter 1: 随机事件及其概率
1. 随机试验,样本点,样本空间 若试验具有下列特点: 在相同条件下可重复进行 每次试验的可能结果不止一个,且所有可能结果在实验前是已知的 实验前不能确定哪一个结果会发生 则称该试验为随机试验,常记为 ...
- Hash中的一些概率计算
Hash是把锋利的刀子,处理海量数据时经常用到,大家可能经常用hash,但hash的有些特点你是否想过.理解过.我们可以利用我们掌握的概率和期望的知识,来分析Hash中一些有趣的问题,比如: 平均每个 ...
- ACM - 概率、期望题目 小结(临时)
概率DP求期望大多数都是全期望公式的运用.主要思考状态空间的划分以及状态事件发生的概率.问题可以分为无环和有环两类.无环一类多数比较简单,可以通过迭代或者记忆化搜索完成.有环一类略复杂,可以通过假设方 ...
- poj 2096 Collecting Bugs (概率dp 天数期望)
题目链接 题意: 一个人受雇于某公司要找出某个软件的bugs和subcomponents,这个软件一共有n个bugs和s个subcomponents,每次他都能同时随机发现1个bug和1个subcom ...
- 《A First Course in Probability》-chaper3-条件概率和独立性-贝叶斯公式、全概率公式
设有事件A.B. 下面结合具体的题目进一步理解这种方法: Q1:保险公司认为人可以分为两类,一类易出事故,另一类则不易出事故.统计表明,一个易出事故者在一年内发生事故的概率是0.4,而对不易出事故者来 ...
- 对Kalman(卡尔曼)滤波器的理解
1.简单介绍(Brief Introduction) 在学习卡尔曼滤波器之前,首先看看为什么叫"卡尔曼". 跟其它著名的理论(比如傅立叶变换.泰勒级数等等)一样.卡尔曼也是一个人的 ...
- MLAPP——概率机器学习知识汇总
<机器学习>课程使用Kevin P. Murphy图书<Machine Learning A Probabilistic Perspective>本英语教材,本书从一个独特的数 ...
随机推荐
- vue框架回顾
- VS2022 17.1.6在windows10下打开winform设计器报timed out while connecting to named pipe错误
.net 6.0的项目,vs2022 17.1.6在windows10下打开winform设计器报timed out while connecting to named pipe错误,同样的项目在wi ...
- ComWin’ round 11部分题解
https://vjudge.net/contest/325913#overview A.Threehouses 题意:一直二维平面上的$n$个点中,前$e$个点落在小岛周围,并且有$p$条边已经连接 ...
- 2022-05-20内部群每日三题-清辉PMP
1.一位团队成员通知项目经理有一个问题可能会破坏项目.项目经理将该问题添加到问题日志中,并要求团队找到解决方案. 项目经理下一步应该怎么做? A.更新风险登记册 B.修订项目管理计划 C.确定适当的风 ...
- spring 理念与项目构建
spring理念: 使现有的技术更容易使用,其本身是一个大杂烩,整合了现有的技术框架. ssh: struct2 spring hibernate ssm :springmvc spring myba ...
- winform 子控件触发父控件事件
private void circlePanel_Click(object sender, EventArgs e) { var panel=sender as UIPanel; if (panel. ...
- Visual Studio Code 如何设置成中文语言
Visual Studio Code 是一款微软的代码编辑器,这款软件是比较不错的,用起来也比较方便,但是好多人在第一次安装的时候展现的是英文的,这对于一些小伙伴是比较头疼的问题,那如何调整为中文的呢 ...
- Centos 7 环境 安装todesk异常
按照todesk官网安装步骤安装. 其实就两步就完成了,在自己虚拟机centos7环境下测试一切正常,但正式环境centos7.9环境下能安装,但安装完打不开,感觉是内核版本的问题. Todesk-- ...
- Linux 第七节(LVM,网卡配置)
LVM 逻辑卷管理器: 解决分区灵活调整大小问题 PV 物理卷 VG 卷组 LV 逻辑卷 pvcreate /dev/sdc vgcreate xiaochong /dev/sdb /dev/sdc ...
- 光盘实现半自动化安装linux以及PXE实现自动安装
重点 实验一:使用 kickstart 半自动化安装CentOS系统 可以将定制安装光盘,并结合kickstart实现基于光盘启动的半自动化安装 实现过程 首先下载httpd搭建个web网页 [ro ...
