[ 赛后总结 ] CSP-J 2022

前言

今年没考好，估分 100+60+0+10=170pts ，大概能混个2=，没什么用。

这下好了，期中也砸了，已经排到全校 30 开外了，果然鱼和熊掌不可兼得，况且我双双落空，接下来怕是想搞也搞不了了，写完这篇，卷 whk 去。

语文	数学	英语	物理	化学	历史	政治	total
108	145	139	58	80	97	78	705

正文

T1 [CSP-J 2022] 乘方

简化题意：给出两个正整数 $a,b(a,b\leqslant10^9)$ ，检查 $a^b(a^b\leqslant10^{18})$ 是否超出 int 类型，即 $10^9$ 或 $2^{31}-1$ ，超过则输出 -1，否则输出该值。

乱搞100pts?

乍一看，不知道是不是有人跟我一样，想到 pow 函数。（可能你们都第一时间放弃这个想法）

于是乎我立马把程序打了出来，当然，还需考虑一下 pow 溢出出现负数的情况。（但后来 tx 说难道不会负负得正吗，我想都溢出了还会继续调用函数计算吗，eee）

点击查看代码

#include<bits/stdc++.h>

using namespace std;

const long long inf=1e9;

long long a,b,ans;

int main()

{

	//freopen("pow.in","r",stdin);

	//freopen("pow.out","w",stdout);

	cin>>a>>b;

	ans=pow(a,b);

	if(ans>inf || ans<0) cout<<-1;

	else cout<<ans;

	return 0;

}

后来洛谷和小图灵实测都是 AC ，我也很恍惚，有人说要特判 $a=1$ 的情况，但我的代码也没超时，有点玄学。

正解

其实就是暴力，一个 for 循环加特判解决的事，考场上我以为它会超时，后来想想，其实不然，只需每次做跟着判断即可。

∵ $10^9=2^{31}-1$ ，

∴当 $a=2$时，此做法循环次数最多 30 次，

则当 $2<a\leqslant10^9$，次数只会趋近于 1 。

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

const ll inf=1e9;

ll a,b;

int main()

{

	//freopen("pow.in","r",stdin);

	//freopen("pow.out","w",stdout);

	cin>>a>>b;

	if(a==1)

	{

		cout<<1;

		return 0;

	}

	ll ans=a;

	for(int i=1;i<=b-1;i++)

	{

		ans*=a;

		if(ans>inf)

		{

			cout<<-1;

			return 0;

		}

	}

	cout<<ans;

	return 0;

}

当然，也有人说可以用快速幂，以后学了再来补。

T2 [CSP-J 2022] 解密

给定一个正整数 $k(k\leqslant10^5)$ ，有 $k$ 次询问，每次给定三个正整数 $n_i,d_i,e_i(n_i\leqslant10^{18})$ ，求两个正整数 $p_i,q_i$ ，使 $n_i=p_i\times q_i~,~d_i\times e_i=(p_i-1)(q_i-1)-1$ ，为了统一，应当保证 $p_i\leqslant q_i$ 。

其中，$d_i\times e_i\leqslant 10^{18}$，设 $m=n-d\times e+2$ ，则有 $m\leqslant10^9$。

正解

一道数学题。良心的是，$m$ 的定义是原题就有的，这引导我们的思路。

分别设等式为1，2式，可变形2式：

\[de=(p-1)(q-1)+1
\]

\[de=pq-p-q+2
\]

\[p+q=pq-de+2
\]

即$$p+q=m$$

联立1得：

\[\begin{cases}
pq=n
\\p+q=m
\end{cases}
\]

这下好办了，带入近似解一个一元二次方程，用公式法即可。

根据方程组，可得：

\[(m-q)q=n
\]

\[q^2-mq+n=0
\]

\[q_1={m-\sqrt{m^2-4n} \over 2},q_2={m+\sqrt{m^2-4n} \over 2}
\]

显然按要求， $p=q_1,q=q_2$ 。

至此，得到答案的由来，当然还需注意一些问题：

众所周知，当 $\Delta<0$ 时，是没有实数根的，此处要提前特判；
得到两个实数根后，显然要判断是否同时满足两个等式；
特别注意（其实我在这里想了很久才明白），两个实数根要求是正整数，说明浮点类型的解也是不合法的。首先，能确定 $n,d,e,p,q,\Delta$ 都是long long，但 $\sqrt{\Delta}$ 就可能出现小数，那么它就有必要是double类型的。显然，如果 $\sqrt{\Delta}$是浮点数，则 ${(\sqrt{\Delta})}^2 \not =\sqrt{\Delta}$，必定会有精度偏差，是整数则不然。

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

int k;

ll n,e,d,m,p,q;

int main()

{

	//freopen("decode.in","r",stdin);

	//freopen("decode.out","w",stdout);

	cin>>k;

	while(k--)

	{

		cin>>n>>d>>e;

		m=n-e*d+2;

		ll delta=m*m-4*n;

		if(delta<0)

		{

			cout<<"NO"<<endl;

			continue;

		}

		double tmp=sqrt(delta);

		p=(m-tmp)/2;

		q=(m+tmp)/2;

		if(tmp*tmp!=delta || p+q!=m || p*q!=n) cout<<"NO"<<endl;

		else cout<<p<<' '<<q<<endl;

	}

	return 0;

}

其实，我考场上写的不是正解，从估分看的出来，是一个只能拿 60pts 的超时程序。

我当时想到了这个 $O(k\times \sqrt{n})$ 的暴力，想着拿个 60pts 算了，因为我虽然 whk 的数学还不错，但 $OI$ 的数论真的把我难吐了，我一直都很抵制做数论题（以后要改了），所以就......没想到正解就是这学期学的，呜呜呜~

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

int k;

ll n,e,d,p,q;

int main()

{

	//freopen("decode.in","r",stdin);

	//freopen("decode.out","w",stdout);

	cin.tie(0);

	cout.tie(0);

	cin>>k;

	while(k--)

	{

		cin>>n>>d>>e;

		ll add=n-e*d+2;

		bool flag=false;

		if(n>1e9)

		{

			for(int i=1e7;i<=sqrt(n);i++)

			//PS：当时以为能降低一点大数据的复杂度，其实并没用

			{

				if(n%i==0)

				{

					p=i;

					q=n/i;

					if(p+q==add)

					{

						cout<<p<<' '<<q<<endl;

						flag=true;

						break;

					}

				}

			}

		}

		else

		{

			for(int i=1;i<=sqrt(n);i++)

			{

				if(n%i==0)

				{

					p=i;

					q=n/i;

					if(p+q==add)

					{

						cout<<p<<' '<<q<<endl;

						flag=true;

						break;

					}

				}

			}

		}

		if(flag) continue;

		cout<<"NO"<<endl;

	}

	return 0;

}

还有用二分做的，我感觉没这必要了吧。

T3 [CSP-J 2022] 逻辑表达式

简化题意：给定一个逻辑表达式字符串 $s$ ,规定在运算时，括号内的部分先运算；两种运算并列时， & 运算优先于 | 运算；同种运算并列时，从左向右运算。

计算它的值。并且统计两种“短路”的次数，定义 & 短路形如 0&x ， | 短路形如1|x ，特别注意，如果某处“短路”包含在更外层被“短路”的部分内则不被统计。

其中，长度 $\leqslant 10^6$ ，保证没有重复的括号嵌套，仅含有字符 0 1 & | ( ) 。

正解

鸽。

T4 [CSP-J 2022] 上升点列

简化题意：在二维平面中，给定 $n$ 个点和 $k$ 个自由添加的点，求在 $n+k$ 个点中，最长子序列的点数，定义该序列为相邻点距离为1，且横纵坐标不下降。

其中，$1 \leq n \leq 500$，$0 \leq k \leq 100$。对于所有给定的整点，其横纵坐标 $1 \leq x_i, y_i \leq {10}^9$，且保证所有给定的点互不重合。对于自由添加的整点，其横纵坐标不受限制。

测试点编号	$n \leq$	$k \leq$	$x_i,y_i \leq$
$1 \sim 2$	$10$	$0$	$10$
$3 \sim 4$	$10$	$100$	$100$
$5 \sim 7$	$500$	$0$	$100$
$8 \sim 10$	$500$	$0$	${10}^9$
$11 \sim 15$	$500$	$100$	$100$
$16 \sim 20$	$500$	$100$	${10}^9$

乱搞25pts

我打个暴搜都只能骗到这点分，可见我水平是何等的低。（甚至是优化了考场10pts的程序）

思路羞于多讲，就是分了 $k=0$ 的特殊情况，一般地，贪心找最左下角点开始查找关于横纵坐标的最长不下降序列；特别地，找最大符合前文性质的联通快。

点击查看代码

#include<bits/stdc++.h>

using namespace std;

const int N=510,M=100;

int n,k;

struct node

{

	int X,Y;

}a[N];

int dx[2]={1,0};

int dy[2]={0,1};

int G[M+10][M+10],ans=-1;

bool vis[M+10][M+10];

bool cmp(node a,node b)

{

	if(a.X==b.X) return a.Y<b.Y;

	return a.X<b.X;

}

void dfs(int x,int y,int now_k,int cnt)

{

	//if(cnt<ans) return;

	if(now_k>k)

	{

		ans=max(ans,cnt);

		return;

	}

	//cout<<x<<' '<<y<<' '<<now_k<<' '<<cnt<<endl<<endl;

	for(int i=0;i<2;i++)

	{

		int tx=x+dx[i],ty=y+dy[i];

		if((tx>=1&&tx<=M&&ty>=1&&ty<=M) && !vis[tx][ty])

		{

			vis[tx][ty]=true;

			if(G[tx][ty]==1)

			{

				dfs(tx,ty,now_k,cnt+1);

			}

			else

			{

				dfs(tx,ty,now_k+1,cnt+1);

			}

			//vis[tx][ty]=false;我服了，找了一个小时

		}

	}

}

void dfs2(int x,int y,int cnt)

{

	ans=max(ans,cnt);

	for(int i=0;i<2;i++)

	{

		int tx=x+dx[i],ty=y+dy[i];

		if((tx>=1&&tx<=M&&ty>=1&&ty<=M) && !vis[tx][ty] && G[tx][ty]==1)

		{

			vis[tx][ty]=true;

			dfs2(tx,ty,cnt+1);

			vis[tx][ty]=false;

		}

	}

}

int main()

{

	//freopen("point.in","r",stdin);

	//freopen("point.out","w",stdout);

	cin.tie(0);

	cin>>n>>k;

	for(int i=1;i<=n;i++)

	{

		cin>>a[i].X>>a[i].Y;

		G[a[i].X][a[i].Y]=1;

	}

	sort(a,a+n+1,cmp);

	//cout<<a[1].X<<' '<<a[1].Y; return 0;

	if(k>0)

		dfs(a[1].X,a[1].Y,0,1);

	else

	{

		int maxn=-1;

		for(int i=1;i<=n;i++)

		{

			memset(vis,false,sizeof(vis));

			ans=-1;

			dfs2(a[i].X,a[i].Y,1);

			maxn=max(maxn,ans);

		}

		cout<<maxn;

		return 0;

	}

	cout<<ans;

	return 0;

}

正解

一道 DP 。其实我一开始看到这道题类似 LIS ，就想到了，但想不出方程，eee。(话说我当时为什么不直接拿它当 LIS 模板做，这样还能拿 65pts ，失策了)

首先，考虑对 $n$ 个节点排序，使其从前往后访问横纵坐标不降（即访问顺序为 $Oxy$ 中从 $O$ 出发， $y=kx(k>0)$ 的第一象限图像），保证转移时无后效性。

状态

可以类比增加一维，用 $f[i][l]$ 表示以 $a_i$ 为结尾，已经插入 $l$ 个额外点的最长不下降子序列的最大点数。
阶段

显然要对 $a_i(1\leqslant i \leqslant n)$ 查找；
当前点的长度是由之前的点转移而得，∴要对 $a_j(1\leqslant j<i)$ 查找；
对于区间 $[a[i],b[i]]$ ，中间可以插入 $len(下界)$ 到 $k$ 个额外点，∴要枚举所有可行的插入方案。

对于 $len$ ，已知两点坐标，可知两点之间最少需要的额外点：

\[len=(a[i].x-a[j].x)+(a[i].y-a[j].y)-1
\]

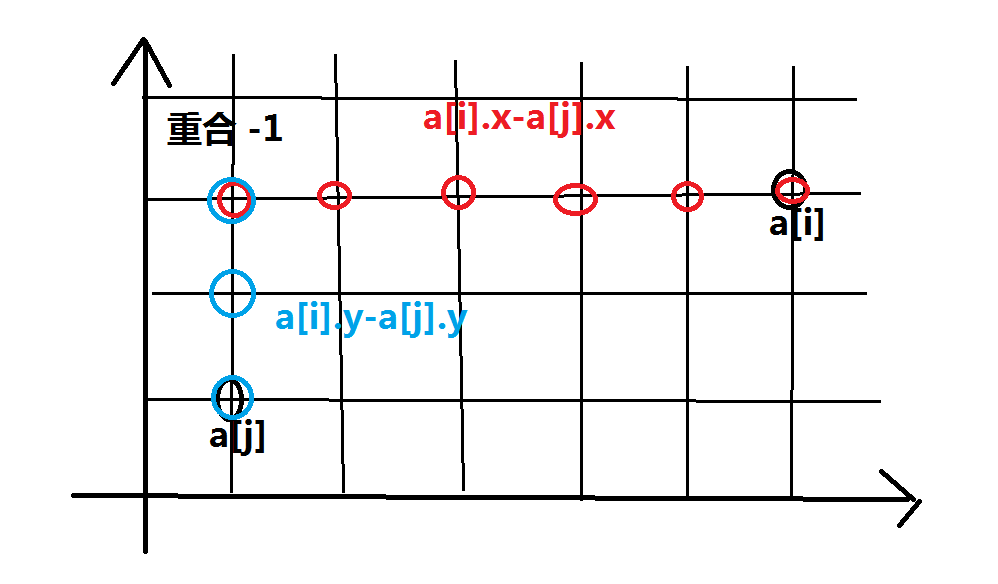
方程

综上易得：

\[f[i][l]=\max_{1\leqslant i\leqslant n,1\leqslant j<i,len \leqslant l\leqslant k}(f[i][l],f[j][l-len]+len+1)
\]

边界

我们初始无法确定 $n$ 个点之间的关系，但可以确定每个点和 $k$ 个点的关系，相当于，在一开始， $k$ 个点可以分别和每个点链接组成保证合法的序列,则有：

\[f[i][j]=j+1
\]

目标

显然，插入所有 $k$ 个点为最优解，即：

\[\max_{1\leqslant i \leqslant n}(f[i][k])
\]

#include<bits/stdc++.h>

using namespace std;

const int N=510,K=110;

struct node

{

	int x,y;

}a[N];

int n,k,f[N][K],ans=-1;

bool cmp(node p,node q)

{

	if(p.x==q.x) return p.y<q.y;

	return p.x<q.x;

}

int main()

{

	//freopen("point.in","r",stdin);

	//freopen("point.out","w",stdout);

	cin>>n>>k;

	for(int i=1;i<=n;i++) cin>>a[i].x>>a[i].y;

	sort(a+1,a+n+1,cmp);

	for(int i=1;i<=n;i++)

		for(int j=0;j<=k;j++) f[i][j]=j+1;

	for(int i=2;i<=n;i++)

		for(int j=i-1;j>=1;j--)

		{

			if(a[j].y>a[i].y)continue;//注意，因为cmp函数按x优先

			int len=(a[i].x-a[j].x)+(a[i].y-a[j].y)-1;

			for(int l=len;l<=k;l++) f[i][l]=max(f[i][l],f[j][l-len]+len+1);

		}

	for(int i=1;i<=n;i++)

		ans=max(ans,f[i][k]);

	cout<<ans;

	return 0;

}

PS

update：2022.11.8

CCF官方数据修正： 100+60+0+20=180pts , $[15.2\%,16.6\%]$ ,还是很慌。
update：2022.11.17

喜提1=，HN分数线170，压线过。