linux服务器下 conda 配置清华源

1. 安装miniconda

• 下载安装脚本

  wget https://mirrors.tuna.tsinghua.edu.cn/anaconda/miniconda/Miniconda3-latest-Linux-x86_64.sh --no-check-certificate
  
  

• 执行安装过程
  
  root@ldk:~# sh Miniconda3-latest-Linux-x86_64.sh
  
  
  
  
  
  
  
  
  
  
  
  

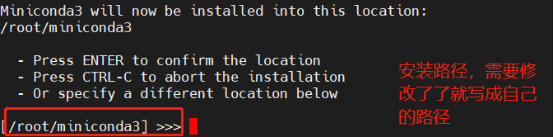
• 取消开机自动启动conda base环境

   conda config --set auto_activate_base false 
  

1. 修改配置文件

   vim /root/.condarc
   (py390) [root@analysisdb Test]#vim /root/.condarc 
   
   channels:
     - defaults
   default_channels:
     - https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main
     - https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/r
     - https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/msys2
   custom_channels:
     conda-forge: https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud
     msys2: https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud
     bioconda: https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud
     menpo: https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud
     pytorch: https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud
     pytorch-lts: https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud
     simpleitk: https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud
   
   auto_activate_base: false
   show_channel_urls: true
   ssl_verify: false
   

   • 注意：show_channel_urls: True这个参数可以设置为false来隐藏源的url

2. 使用说明

• 创建虚拟环境py39

  conda create --name py39 python=3.9
  

• 常用命令

  # 查看所有的虚拟环境
  conda env list 
  
  # 查看默认环境中安装了哪些包
  conda list 
  
  # 查看指定的环境中安装了哪些包
  conda list -n py39
  
  # 移除虚拟环境py39
  conda remove --name py39 --all
  
  # 进入虚拟环境py39
  conda activate py39
  
  # 退出虚拟环境py39
  conda deactivate
  
  # 移除源
  conda config --remove channels