算法笔记--FFT

推荐阅读资料：算法导论第30章

本文不做证明，详细证明请看如上资料。

FFT在算法竞赛中主要用来加速多项式的乘法

普通是多项式乘法时间复杂度的是O(n²)，而用FFT求多项式的乘法可以使时间复杂度达到O(nlogn)

FFT求多项式的乘法步骤主要如下图

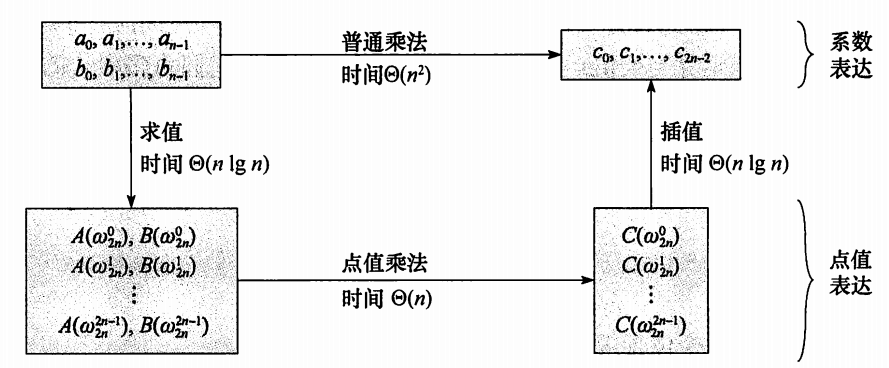
其中求值是将系数表达转换成点值表达，带入的自变量是wⁿ=1的复数解，称为DFT

插值是将点值表达转换成系数表达，称为DFT^-1

DFT 和 DFT^-1都可以用FFT加速实现

这是递归版的FFT

还有一种非递归的版本

我们发现叶子节点的下表的二进制为：000   100   010   110    001  101   110    111

与它们的本身所对应的位置的二进制：000   001  010   011    100   101    011   111

相反

所以我们可以确定叶子节点的值，从下往上进行操作

求二进制反转的代码(其中L是二进制位):

for (int i = ; i < n; i++) {
            R[i] = (R[i>>]>>) | ((i&) << L-);
        }

假设现在R[i]的二进制是abcd，没有操作之前的R[i>>1]是0abc,操作之后的是cba0，再右移是0cba,再判断原来的d是不是1在最高位放1或0，就刚好是反转的结果

模板：

递归版（以求大数乘法为例）：

#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define pi acos(-1.0)
#define LL long long
#define mp make_pair
#define pb push_back
#define ls rt<<1, l, m
#define rs rt<<1|1, m+1, r
#define ULL unsigned LL
#define pll pair<LL, LL>
#define pii pair<int, int>
#define piii pair<int,pii>
#define mem(a, b) memset(a, b, sizeof(a))
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define fopen freopen("in.txt", "r", stdin);freopen("out.txt", "w", stout);
//head

typedef complex<double> cd;
const int N = 2e5 + ;
char a[N], b[N];
cd A[N], B[N];
int tmp[N];
void fft(cd *x, int n, int type) {
    if(n == ) return ;
    cd l[n>>], r[n>>];
    for (int i = ; i < n; i += ) {
        l[i>>] = x[i];
        r[i>>] = x[i+];
    }
    fft(l, n>>, type);
    fft(r, n>>, type);
    cd wn(cos(*pi/n), sin(type**pi/n)), w(, ), t;
    for(int i = ; i < n>>; i++, w *= wn) {
        t = w*r[i];
        x[i] = l[i] + t;
        x[i+(n>>)] = l[i] - t;
    }
}
int main() {
    while(~scanf("%s%s", a, b)) {
        int n = strlen(a), m = strlen(b);
        mem(A, );
        mem(B, );
        mem(tmp, );
        for (int i = n - ; i >= ; i--) A[n--i] = a[i] - '';
        for (int i = m - ; i >= ; i--) B[m--i] = b[i] - '';
        m = m + n;
        for(n = ; n <= m; n <<= );
        fft(A, n, );
        fft(B, n, );
        for (int i = ; i < n; i++) A[i] *= B[i];
        fft(A, n, -);
        for (int i = ; i < m; i++) {
            int t = (int)(A[i].real()/n + 0.5);
            t += tmp[i];
            tmp[i] = t%;
            tmp[i+] += t/;
        }
        int i;
        for (i = m; i >= ; i--) if(tmp[i]) break;
        for (i; i >= ; i--) printf("%d", tmp[i]);
        printf("\n");
    }
    return ;
}

FFT非递归版模板：

typedef complex<double> cd;
const int N = 2e5 + ;
cd A[N], B[N];
int R[N];
void fft(cd *x, int n, int type) {
    for (int i = ; i < n; i++) if(i < R[i]) swap(x[i], x[R[i]]);
    for (int i = ; i < n; i <<= ) {
        cd wn(cos(pi/i), type*sin(pi/i));
        for (int j = ; j < n; j += i<<) {
            cd w(, );
            for (int k = ; k < i; k++, w*=wn) {
                cd X = x[j+k], Y = w*x[j+k+i];
                x[j+k] = X+Y;
                x[j+k+i] = X-Y;
            }
        }
    }
    if(type == -) {
        for (int i = ; i < n; ++i) x[i]=(x[i].real()/n,x[i].imag());
    }
}

int main() {
    int n, m, L = ;
    scanf("%d %d", &n, &m);
    for (int i = ; i < n; ++i) scanf("%d", &A[i]);
    for (int i = ; i < m; ++i) scanf("%d", &B[i]);
    m = m + n;
    for(n = ; n <= m; n <<= ) L++;
    for (int i = ; i < n; i++) R[i] = (R[i>>]>>) | ((i&) << L-);
    fft(A, n, );
    fft(B, n, );
    for (int i = ; i < n; i++) A[i] *= B[i];
    fft(A, n, -);
    for (int i = ; i < m; i++) printf("%d\n", (int)(A[i].real()+0.5));
    return ;
}

PS:手写complex类+非递归版最快

NTT模板：

#include<bits/stdc++.h>
using namespace std;
/*
469762049--3
998244353--3
1004535809--3
1e9+7 -- 5
（g 是mod(r*2^k+1)的原根）
素数  r  k  g
3   1   1   2
5   1   2   2
17  1   4   3
97  3   5   5
193 3   6   5
257 1   8   3
7681    15  9   17
12289   3   12  11
40961   5   13  3
65537   1   16  3
786433  3   18  10
5767169 11  19  3
7340033 7   20  3
23068673    11  21  3
104857601   25  22  3
167772161   5   25  3
469762049   7   26  3
1004535809  479 21  3
2013265921  15  27  31
2281701377  17  27  3
3221225473  3   30  5
75161927681 35  31  3
77309411329 9   33  7
*/

const int N = , P = ;
inline int qpow(int x, int y) {
  int res();
  while (y) {
    if (y & ) res = 1ll * res * x % P;
    x = 1ll * x * x % P;
    y >>= ;
  }
  return res;
}

int r[N];
void ntt(int *x, int n, int opt) {
  register int i, j, k, m, gn, g, tmp;
  for (i = ; i < n; ++i)
    if (r[i] < i) swap(x[i], x[r[i]]);
  for (m = ; m <= n; m <<= ) {
    k = m >> ;
    gn = qpow(, (P - ) / m);    ///3是原根
    for (i = ; i < n; i += m) {
      g = ;
      for (j = ; j < k; ++j, g = 1ll * g * gn % P) {
        tmp = 1ll * x[i + j + k] * g % P;
        x[i + j + k] = (x[i + j] - tmp + P) % P;
        x[i + j] = (x[i + j] + tmp) % P;
      }
    }
  }
  if (opt == -) {
    reverse(x + , x + n);
    register int inv = qpow(n, P - );
    for (i = ; i < n; ++i) x[i] = 1ll * x[i] * inv % P;
  }
}

int A[N], B[N], C[N];

int main() {
    int n, m, L = ;
    scanf("%d %d", &n, &m);
    ++n, ++m;
    for (int i = ; i < n; ++i) scanf("%d", &A[i]);
    for (int i = ; i < m; ++i) scanf("%d", &B[i]);
    m = m + n;
    for(n = ; n <= m; n <<= ) L++;
    for (int i = ; i < n; i++) r[i] = (r[i>>]>>) | ((i&) << L-);
    ntt(A, n, );
    ntt(B, n, );
    for (int i = ; i < n; ++i) C[i] = 1ll * A[i] * B[i] % P;
    ntt(C, n, -);
    for (int i = ; i < m-; ++i) printf("%d ", C[i]);
    puts("");
    return ;
}

任意模数NTT模板：

const int maxn = ,maxm = ;
int pr[]={,,};
int R[maxn];
inline LL qpow(LL a,LL b,LL p){
    LL re = ; a %= p;
    for (; b; b >>= ,a = a * a % p)
        if (b & ) re = re * a % p;
    return re;
}
struct FFT{
    int G,P,A[maxn];
    void NTT(int* a,int n,int f){
        for (int i = ; i < n; i++) if (i < R[i]) swap(a[i],a[R[i]]);
        for (int i = ; i < n; i <<= ){
            int gn = qpow(G,(P - ) / (i << ),P);
            for (int j = ; j < n; j += (i << )){
                int g = ,x,y;
                for (int k = ; k < i; k++,g = 1ll * g * gn % P){
                    x = a[j + k],y = 1ll * g * a[j + k + i] % P;
                    a[j + k] = (x + y) % P,a[j + k + i] = (x + P - y) % P;
                }
            }
        }
        if (f == ) return;
        int nv = qpow(n,P - ,P); reverse(a + ,a + n);
        for (int i = ; i < n; i++) a[i] = 1ll * a[i] * nv % P;
    }
}fft[];
int F[maxn],G[maxn],B[maxn],deg1,deg2,deg,md;
LL ans[maxn];
LL inv(LL n,LL p){return qpow(n % p,p - ,p);}
LL mul(LL a,LL b,LL p){
    LL re = ;
    for (; b; b >>= ,a = (a + a) % p)
        if (b & ) re = (re + a) % p;
    return re;
}
void CRT(){
    deg = deg1 + deg2;
    LL a,b,c,t,k,M = 1ll * pr[] * pr[];
    LL inv1 = inv(pr[],pr[]),inv0 = inv(pr[],pr[]),inv3 = inv(M % pr[],pr[]);
    for (int i = ; i <= deg; i++){
        a = fft[].A[i],b = fft[].A[i],c = fft[].A[i];
        t = (mul(a * pr[] % M,inv1,M) + mul(b * pr[] % M,inv0,M)) % M;
        k = ((c - t % pr[]) % pr[] + pr[]) % pr[] * inv3 % pr[];
        ans[i] = ((k % md) * (M % md) % md + t % md) % md;
    }
}
void conv(){
    int n = ,L = ;
    while (n <= (deg1 + deg2)) n <<= ,L++;
    for (int i = ; i < n; i++) R[i] = (R[i >> ] >> ) | ((i & ) << (L - ));
    for (int u = ; u <= ; u++){
        fft[u].G = ; fft[u].P = pr[u];
        for (int i = ; i <= deg1; i++) fft[u].A[i] = F[i];
        for (int i = ; i <= deg2; i++) B[i] = G[i];
        for (int i = deg2 + ; i < n; i++) B[i] = ;
        fft[u].NTT(fft[u].A,n,); fft[u].NTT(B,n,);
        for (int i = ; i < n; i++) fft[u].A[i] = 1ll * fft[u].A[i] * B[i] % pr[u];
        fft[u].NTT(fft[u].A,n,-);
    }
}
int main(){
    scanf("%d %d %d", &deg1, &deg2, &md);
    for (int i = ; i <= deg1; i++) scanf("%d", &F[i]);
    for (int i = ; i <= deg2; i++) scanf("%d", &G[i]);
    conv(); CRT();
    for (int i = ; i <= deg; i++) printf("%lld ",ans[i]);
    return ;
}