[UE4]在AIController中使用行为树
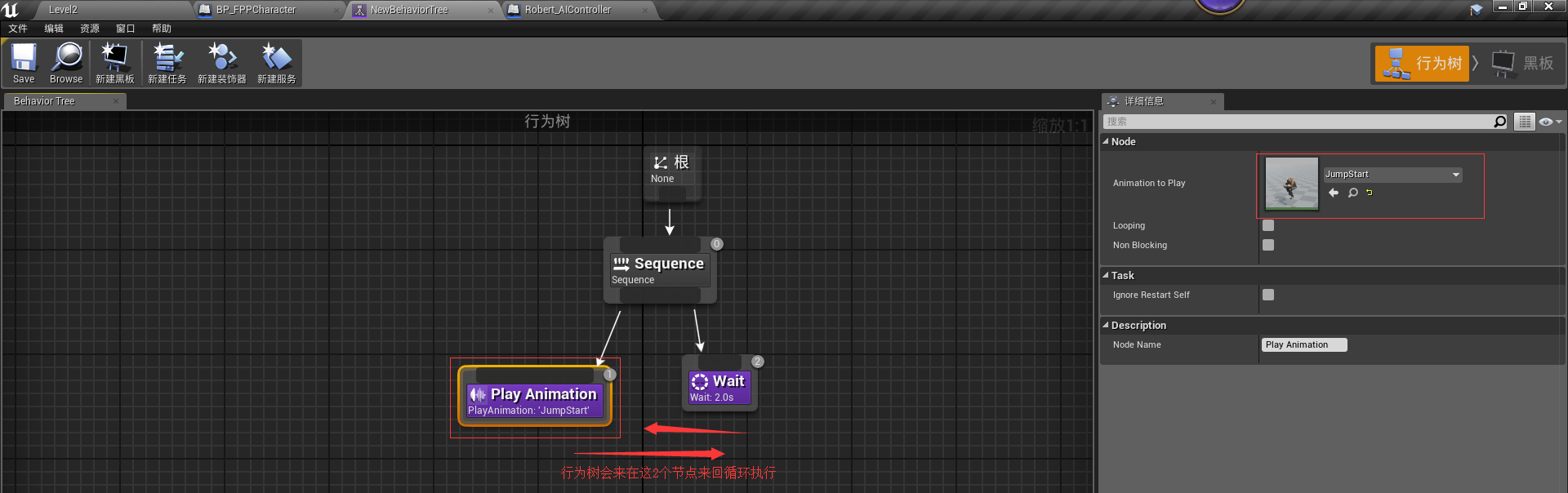
行为树会在Root根下面的每个子节点中从左右到右来回往复循环执行。
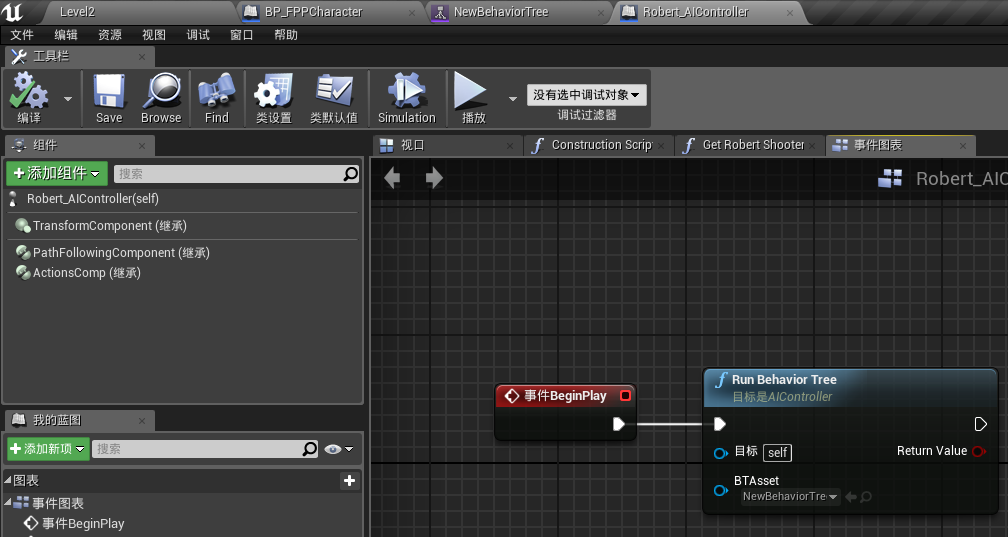
[UE4]在AIController中使用行为树的更多相关文章
- lintcode :前序遍历和中序遍历树构造二叉树
解题 前序遍历和中序遍历树构造二叉树 根据前序遍历和中序遍历树构造二叉树. 样例 给出中序遍历:[1,2,3]和前序遍历:[2,1,3]. 返回如下的树: 2 / \ 1 3 注意 你可以假设树中不存 ...
- 如何将数据库中存的树转化为树形列表(以easyui的tree为例)
很多时候,我们会把一棵树存放到数据库中,当前台需要展示一个树形列表时,将这棵树读取出来并显示,这个过程是怎么实现的呢? 这篇文章是以构造一棵easyui前台框架的一个树形列表为例,后台框架是sprin ...
- WPF中的逻辑树和可视化树
WPF中的逻辑树是指XAML元素级别的嵌套关系,逻辑树中的节点对应着XAML中的元素. 为了方便地自定义控件模板,WPF在逻辑树的基础上进一步细化,形成了一个“可视化树(Visual Tree)”,树 ...
- 改造一下jeecg中的部门树
假装有需求 关于 jeecg 提供的部门树,相信很多小伙伴都已经用过了,今天假装有那么一个需求 "部门树弹窗选择默认展开下级部门",带着这个需求再次去探索一下吧. 一.改造之前的部 ...
- LintCode-73.前序遍历和中序遍历树构造二叉树
前序遍历和中序遍历树构造二叉树 根据前序遍历和中序遍历树构造二叉树. 注意事项 你可以假设树中不存在相同数值的节点 样例 给出中序遍历:[1,2,3]和前序遍历:[2,1,3]. 返回如下的树: ...
- 利用树的先序和后序遍历打印 os 中的目录树
[0]README 0.1)本代码均为原创,旨在将树的遍历应用一下下以加深印象而已:(回答了学习树的遍历到底有什么用的问题?)你对比下linux 中的文件树 和我的打印结果就明理了: 0.2)我们采用 ...
- 理解WPF中的视觉树和逻辑树
轉載地址:http://blog.csdn.net/changtianshuiyue/article/details/26981797 理解WPF中的视觉树和逻辑树 Understanding th ...
- [leetcode/lintcode 题解] 前序遍历和中序遍历树构造二叉树
[题目描述] 根据前序遍历和中序遍历树构造二叉树. 在线评测地址: https://www.jiuzhang.com/solution/construct-binary-tree-from-preor ...
- 谈谈InnoDB中的B+树索引
索引类似于书的目录,他是帮助我们从大量数据中快速定位某一条或者某个范围数据的一种数据结构.有序数组,搜索树都可以被用作索引.MySQL中有三大索引,分别是B+树索引.Hash索引.全文索引.B+树索引 ...
随机推荐
- webpack 搭建问题汇总
总结一下遇到的问题: 1.这样的警告(The 'mode' option has not been set, webpack will fallback to 'production' for thi ...
- madlib centos yum 包安装
使用centos 测试安装madlib sql 机器学习类库 安装步骤 添加pg 10 repo yum install https://download.postgresql.org/pub/rep ...
- oracle-闪回技术2
闪回版本查询,用到了附加日志 闪回事务查询 http://blog.csdn.net/laoshangxyc/article/details/12405459 这个博客的备份与恢复可以参考 ##### ...
- phpstorm破解方法
方法1:打开网址 http://idea.lanyus.com/ 选择获取注册码,复制生成的验证码 安装完成后,打开软件,依次选择菜单栏 Help -> Register-> Activa ...
- centos7下git服务器端搭建(转)
git的安装: yum 源仓库里的 Git 版本更新不及时,最新版本的 Git 是 1.8.3.1,但是官方最新版本已经到了 2.9.2.想要安装最新版本的的 Git,只能下载源码进行安装. 1. 查 ...
- RedHat如何关闭防火墙 : http://blog.csdn.net/chongxin1/article/details/76072758
版本号:RedHat6.5 JDK1.8 Hadoop2.7.3 hadoop 说明:从版本2开始加入了Yarn这个资源管理器,Yarn并不需要单独安装.只要在机器上安装了JDK就可以直接安 ...
- 有10 亿个 url,每个 url 大小小于 56B,要求去重,内存只给你4G
问题:有10 亿个 url,每个 url 大小小于 56B,要求去重,内存只给你4G 思路: 1.首先将给定的url调用hash方法计算出对应的hash的value,在10亿的url中相同url必然有 ...
- JDK1.8中如何用ScriptEngine动态执行JS
JDK1.8中如何用ScriptEngine动态执行JS jdk1.6开始就提供了动态脚本语言诸如JavaScript动态的支持.这无疑是一个很好的功能,毕竟Java的语法不是适合成为动态语言.而JD ...
- WyBox使用shell脚本检测io口是否正常
1. 修改mt7620a.dts文件,把gpio管脚复用全都定义为通用gpio /dts-v1/; /include/ "mt7620a.dtsi" / { compatible ...
- 关于AXI4-Stream to Video Out 和 Video Timing Controller IP核学习
关于AXI4-Stream to Video Out 和 Video Timing Controller IP核学习 1.AXI4‐Stream to Video Out Top‐Level Sign ...
