Codeforces 833A The Meaningless Game - 数论 - 牛顿迭代法 - 二分法

Slastyona and her loyal dog Pushok are playing a meaningless game that is indeed very interesting.

The game consists of multiple rounds. Its rules are very simple: in each round, a natural number k is chosen. Then, the one who says (or barks) it faster than the other wins the round. After that, the winner's score is multiplied by k2, and the loser's score is multiplied by k. In the beginning of the game, both Slastyona and Pushok have scores equal to one.

Unfortunately, Slastyona had lost her notepad where the history of all n games was recorded. She managed to recall the final results for each games, though, but all of her memories of them are vague. Help Slastyona verify their correctness, or, to put it another way, for each given pair of scores determine whether it was possible for a game to finish with such result or not.

Input

In the first string, the number of games n (1 ≤ n ≤ 350000) is given.

Each game is represented by a pair of scores a, b (1 ≤ a, b ≤ 109) – the results of Slastyona and Pushok, correspondingly.

Output

For each pair of scores, answer "Yes" if it's possible for a game to finish with given score, and "No" otherwise.

You can output each letter in arbitrary case (upper or lower).

Example

input

6
2 4
75 45
8 8
16 16
247 994
1000000000 1000000

output

Yes
Yes
Yes
No
No
Yes

Note

First game might have been consisted of one round, in which the number 2 would have been chosen and Pushok would have won.

The second game needs exactly two rounds to finish with such result: in the first one, Slastyona would have said the number 5, and in the second one, Pushok would have barked the number 3.

---

　　题目大意 (题目太简洁不需要大意，看原文吧)

　　对于每组询问等于求这么一个方程组的一组解，判断解是否是整数:

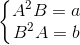
　　首先可以得到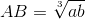，设它为x，那么有

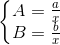
　　显然解是整数解的条件是x为整数且a，b均能被x整除。前半个条件又等价于ab为完全立方数。

　　这个判断嘛。。牛顿迭代去开立方，二分法，HashMap都可以。

　　为了装逼先写了个牛顿迭代，然而大概是我的牛顿迭代常数逆天，所以跑得比较慢。

Code

 /**
  * Codeforces
  * Problem#833A
  * Accepted
  * Time: 468ms
  * Memory: 2100k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;
 #define double long double

 const double eps = 1e-;
 double sqrt3(double x) {
     double r = x;
     double f = , k;
     do {
         f = r * r * r - x;
         k =  * r * r;
         r -= f / k;
     } while (f > eps);
     return r;
 }

 int a, b;
 long long P;
 inline void init() {
     scanf("%d%d", &a, &b);
     P = a * 1LL * b;
 }

 inline boolean solve() {
     long long x = sqrt3(P);
     if(x * x * x != P)    return false;
     return !(a % x || b % x);
 }

 int T;
 int main() {
     scanf("%d", &T);
     while(T--) {
         init();
         puts(solve() ? ("Yes") : ("No"));
     }
     return ;
 }

The Meaningless Game(Newton's Methon)

　　然后写了一个二分法，快了将近一倍。

Code

 /**
  * Codeforces
  * Problem#833A
  * Accepted
  * Time: 218ms
  * Memory: 2052k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;
 #define LL long long

 int sqrt3(LL x) {
     int l = , r = 1e6;
     while(l <= r) {
         LL mid = (l + r) >> ;
         if(mid * mid * mid <= x)    l = mid + ;
         else r = mid - ;
     }
     return l - ;
 }

 int a, b;
 long long P;
 inline void init() {
     scanf("%d%d", &a, &b);
     P = a * 1LL * b;
 }

 inline boolean solve() {
     long long x = sqrt3(P);
     if(x * x * x != P)    return false;
     return !(a % x || b % x);
 }

 int T;
 int main() {
     scanf("%d", &T);
     while(T--) {
         init();
         puts(solve() ? ("Yes") : ("No"));
     }
     return ;
 }

The Meaningless Game(Binary Search)

　　最后写了一个可以用Hash的二分法(Excuse me？新型long long开方向下取整？)

Code

 /**
  * Codeforces
  * Problem#833A
  * Accepted
  * Time: 233ms
  * Memory: 9900k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;
 #define LL long long

 const int limit = 1e6;
 LL arr3[limit + ];
 inline void rinit() {
     for(int i = ; i <= limit; i++)
         arr3[i] = i * 1LL * i * i;
 } 

 int a, b;
 long long P;
 inline void init() {
     scanf("%d%d", &a, &b);
     P = a * 1LL * b;
 }

 inline boolean solve() {
     int x = lower_bound(arr3 + , arr3 + limit + , P) - arr3;
     if(arr3[x] != P)    return false;
     return !(a % x || b % x);
 }

 int T;
 int main() {
     rinit();
     scanf("%d", &T);
     while(T--) {
         init();
         puts(solve() ? ("Yes") : ("No"));
     }
     return ;
 }