PCA whitening
对输入数据 ,维度为2时,想要把数据降维1维:
,维度为2时,想要把数据降维1维:

数据的主方向就是旋转数据的第一维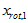 。因此,若想把这数据降到一维,可令:
。因此,若想把这数据降到一维,可令:
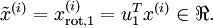
数据已经进行预处理(零均值),使得每个特征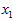 和
和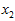 具有相同的均值和方差。
具有相同的均值和方差。
PCA算法将寻找一个低维空间来投影我们的数据。从下图中可以看出, 是数据变化的主方向,而
是数据变化的主方向,而  是次方向。
是次方向。
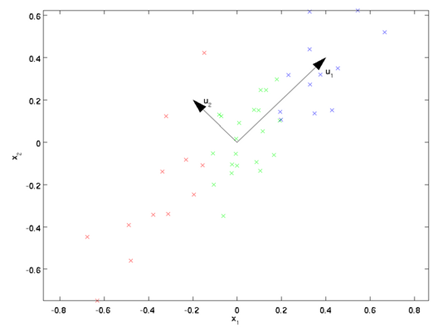
为更形式化地找出方向 和
和 ,我们首先计算出协方差矩阵
,我们首先计算出协方差矩阵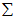 ,如下所示:
,如下所示:

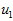 就是协方差矩阵的主特征向量,而
就是协方差矩阵的主特征向量,而 是次特征向量。(按照特征值得大小选取)
是次特征向量。(按照特征值得大小选取)
向量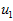 和
和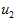 构成了一个新基,可以用来表示数据。那么
构成了一个新基,可以用来表示数据。那么 就是样本点
就是样本点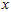 在维度
在维度 上的投影的长度(幅值)。同样的,
上的投影的长度(幅值)。同样的,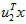 是
是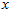 投影到
投影到 维度上的幅值。
维度上的幅值。
在本例中,可得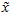 的点图如下(取
的点图如下(取 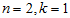 ):
):
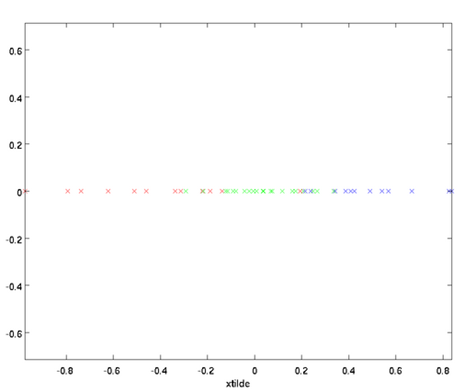
协方差:为了衡量两个数据的相关性,一个数据朝大于均值的方向走的趋势时,另一个数据如果朝小于均值的方向走,趋势相反,协方差值为负的,负相关;如果另一个数据同意朝大于均值的方向变化,协方差为正值,正相关。如果协方差值为0,不相关。
数据白化就是为降低训练数据的冗余,降低输入的冗余性
由前面的例子,特征 的分布如下图所示:
的分布如下图所示:

这个数据的协方差矩阵如下:

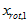 和
和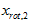 是不相关的, 满足我们对白化结果的第一个要求 (特征间相关性降低)。为了使每个输入特征具有单位方差,我们可以直接使用
是不相关的, 满足我们对白化结果的第一个要求 (特征间相关性降低)。为了使每个输入特征具有单位方差,我们可以直接使用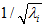 作为缩放因子来缩放每个特征
作为缩放因子来缩放每个特征 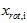 。具体地,我们定义白化后的数据
。具体地,我们定义白化后的数据 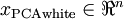 如下:
如下:
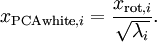
绘制出 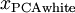 ,我们得到:
,我们得到:

这些数据现在的协方差矩阵为单位矩阵 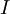 。我们说,
。我们说, 是数据经过PCA白化后的版本:
是数据经过PCA白化后的版本: 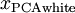 中不同的特征之间不相关并且具有单位方差。
中不同的特征之间不相关并且具有单位方差。
拿图像为例,图像中的像素之间存在很强的相关性。(在图像处理中,一个像素与相邻像素的灰度值之间有联系,所以可以利用这一点进行图像压缩)。白化就是为了减少冗余也就是减少这种相关性。PCA白化在减少特征之间相关性的处理方法与PCA算法相同,找到一个新的基,将数据投影到新的基上,也就是将原始数据做旋转变化,达到减少相关性的目标。但PCA白化与PCA有一点不同,就是处理后的数据的方差为单位方差。主要是将主轴上的数据进行了缩放处理。
ZCA白化是在PCA白化后的数据基础上做处理,主要是对数据进行旋转,使数据比较好的接近原始数据,并没有减少数据特征之间的相关性。
PCA与白化,
就是对输入数据进行预处理,
前者对数据进行降维,后者对数据进行方差处理。
PCA whitening的更多相关文章
- (六)6.8 Neurons Networks implements of PCA ZCA and whitening
PCA 给定一组二维数据,每列十一组样本,共45个样本点 -6.7644914e-01 -6.3089308e-01 -4.8915202e-01 ... -4.4722050e-01 -7.4 ...
- UFLDL教程之(三)PCA and Whitening exercise
Exercise:PCA and Whitening 第0步:数据准备 UFLDL下载的文件中,包含数据集IMAGES_RAW,它是一个512*512*10的矩阵,也就是10幅512*512的图像 ( ...
- Deep Learning学习随记(二)Vectorized、PCA和Whitening
接着上次的记,前面看了稀疏自编码.按照讲义,接下来是Vectorized, 翻译成向量化?暂且这么认为吧. Vectorized: 这节是老师教我们编程技巧了,这个向量化的意思说白了就是利用已经被优化 ...
- CS229 6.8 Neurons Networks implements of PCA ZCA and whitening
PCA 给定一组二维数据,每列十一组样本,共45个样本点 -6.7644914e-01 -6.3089308e-01 -4.8915202e-01 ... -4.4722050e-01 -7.4 ...
- PCA和Whitening
PCA: PCA的具有2个功能,一是维数约简(可以加快算法的训练速度,减小内存消耗等),一是数据的可视化. PCA并不是线性回归,因为线性回归是保证得到的函数是y值方面误差最小,而PCA是保证得到的函 ...
- 【DeepLearning】Exercise:PCA and Whitening
Exercise:PCA and Whitening 习题链接:Exercise:PCA and Whitening pca_gen.m %%============================= ...
- 【转】PCA与Whitening
PCA: PCA的具有2个功能,一是维数约简(可以加快算法的训练速度,减小内存消耗等),一是数据的可视化. PCA并不是线性回归,因为线性回归是保证得到的函数是y值方面误差最小,而PCA是保证得到的函 ...
- DL四(预处理:主成分分析与白化 Preprocessing PCA and Whitening )
预处理:主成分分析与白化 Preprocessing:PCA and Whitening 一主成分分析 PCA 1.1 基本术语 主成分分析 Principal Components Analysis ...
- PCA and Whitening on natural images
Step 0: Prepare data Step 0a: Load data The starter code contains code to load a set of natural imag ...
随机推荐
- 软件工程_10th weeks
不管是什么原因,都没有在周三24:00前发布博客,赶紧用行动补上~ psp DATE START_TIME END_TIME EVENT TYPE DELTA 5.8 9:00 12:00 论 ...
- Delphi中的构造函数的override的问题
TObject的构造方法Create不能被override.因为它是一个静态方法.
- Bootstrap缩略图
前面的话 缩略图在网站中最常用的地方就是产品列表页面,一行显示几张图片,有的在图片底部(左侧或右侧)带有标题.描述等信息.Bootstrap框架将这一部独立成一个模块组件,本文将详细介绍Bootstr ...
- mybatis 一对多的注入 指的是连表查询时候 将不同的查询结果以列表存储对象形式 注入进去 多对一指的是 查询多条结果但都是一样的 只需注入一条
mybatis 一对多的注入 指的是连表查询时候 将不同的查询结果以列表存储对象形式 注入进去 多对一指的是 查询多条结果但都是一样的 只需注入一条
- 关于mysql性能压测之tpcc
软件下载: wget http://imysql.com/wp-content/uploads/2014/09/tpcc-mysql-src.tgz安装依赖:yum install -y mysql- ...
- Coding Contest HDU - 5988(费用流)
题意: 有n个区域和m条路,每个区域有a[i]个人和b[i]个食物,然后是m条路连接两个区域,这条路容量为cap,这条路断掉的概率为p,第一个经过的时候一定不会断,后面的人有概率p会断,现在需要所有人 ...
- MT【227】换钱的总数
(2012复旦)将1张面值100元的人民币全部换成面值1角,2角,5角的人民币,不同的换法有多少种? 解:即求不等式$2x+5y\le1000$的所有非负整数解的个数.由匹克公式:$S=a+\dfra ...
- Leetcode 326.3的幂 By Python
给定一个整数,写一个函数来判断它是否是 3 的幂次方. 示例 1: 输入: 27 输出: true 示例 2: 输入: 0 输出: false 示例 3: 输入: 9 输出: true 示例 4: 输 ...
- 监控(2)-php-fpm进程监控 shell
#!/bin/bash #监控的网页地址url="http://dev2.jwsmed.com" #fastcgi启动/重启/停止脚本路径PROG=/data/fistsoft/p ...
- ECMAScript 6 -- let和const命令
ES6新增了let命令,用来声明变量.它的用法类似于var,但是所声明的变量,只在let命令所在的代码块内有效. for (let i = 0; i ; i++) {console.log(i);} ...
