【LeetCode每天一题】Longest Palindromic Substring(最长回文字串)

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:                             Input: "babad"                         Output: "bab"                      Note: "aba" is also a valid answer.

Example 2:                             Input: "cbbd"                           Output: "bb"

思路：最简单的办法是使用暴力破解法，依此遍历每一个字符（基数情况）和相邻的两个字符（偶数情况）的情况来对比前后是最长相等的字符串，最后返回结果。但是时间复杂度太高为O(n³)，如果字符串太长会直接超时。

　　  第二种是使用动态规划，我们使用辅助数组来存储回文情况，如果在判断P(i, j)时，p(i+1, j-1)时是回文，我们就不用在进行判断，只需要判断S[i] == s[j ]即可。从而减少时间复杂为O(n²), 空间复杂度为O(n²)(空间换时间思路)。

　　 第三种思路是我们从头开始遍历，然后以此为中心考虑基数个数和偶数个数的时候，得出最长字符串的结果。这样复杂度为O(n²),空间复杂度为O(1)。

图示思路

---

　　        

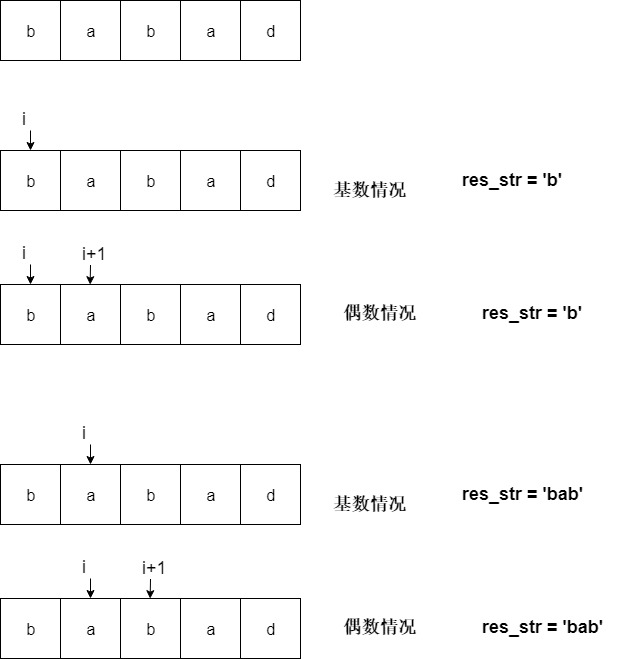
代码解决

---

 class Solution(object):
     def longestPalindrome(self, s):
         """
         :type s: str
         :rtype: str
         """
         if len(s) < :                # 长度小于2直接返回
             return s
         res_str = ''
         for i in range(len(s)):       # 从头开始遍历
             tem = self.find_par(s, i, i)       # 以基数的形式进行查找最长回文

             if len(tem) > len(res_str):         # 比较大小
                 res_str = tem

             tem = self.find_par(s, i, i+)      # 以偶数形式进行查找
             if len(tem) > len(res_str):
                 res_str = tem
         return res_str                             # 返回结果

     def find_par(self, s, start, end):           # 查找函数
         while start >= and end < len(s) and s[start] == s[end]:    # 以当前小标为基准，前后移动，知道不相等或者前后超出范围为止。
             start -=
             end +=
         return s[start+: end]                 # 返回结果字符串