ML: 降维算法-LLE

局部线性嵌入 （Locally linear embedding）是一种非线性降维算法，它能够使降维后的数据较好地保持原有 流形结构 。LLE可以说是流形学习方法最经典的工作之一。很多后续的流形学习、降维方法都与LLE有密切联系。

如下图，使用LLE将三维数据（b）映射到二维（c）之后，映射后的数据仍能保持原有的数据流形（红色的点互相接近，蓝色的也互相接近），说明LLE有效地保持了数据原有的流行结构。

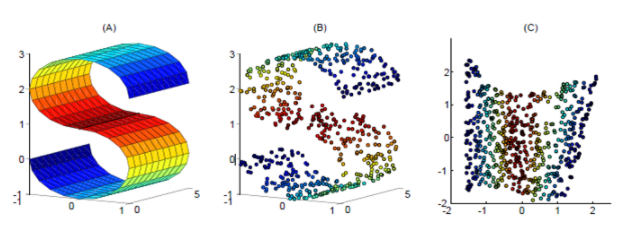
但是LLE在有些情况下也并不适用，如果数据分布在整个封闭的球面上，LLE则不能将它映射到二维空间，且不能保持原有的数据流形。那么我们在处理数据中，首先假设数据不是分布在闭合的球面或者椭球面上。

LLE算法认为每一个数据点都可以由其近邻点的线性加权组合构造得到。算法的主要步骤分为三步：

• 1、寻找每个样本点的k个近邻点；
• 2、由每个 样本点的近邻点计算出该样本点的局部重建权值矩阵；
• 3、由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。

理解：对于图像X中每一个块X1

• 第一步是计算出每个样本点Xi的k个近邻点，即找出样本点的近邻域集合，此处计算可以通过欧几里德距离法求；
• 第二步是计算出样本点的局部重建权值矩阵W来使得重构块X1的误差最小化；
• 第三步将所有样本点映射到低维空间中达到降维的目的

其原理解释可参考：

• http://www.doc88.com/p-50598151896.html
• http://blog.csdn.net/tCDPYh6sA3/article/details/61191617

  R实现LLE算法包

---

R算法包 lle ， 参考资料：https://cran.r-project.org/web/packages/lle/index.html

Usage： lle(X, m, k, reg = 2, ss = FALSE, p = 0.5, id = FALSE, nnk = TRUE, eps = 1, iLLE = FALSE, v = 0.99)

• X: 输入的数据对象
• m: 输入数据的内在维度，这个参数主要影响结果的可视化，实现的内在维度结果在算法中会自动进行计算
• k: 近邻个数，K的取值在算法中起到关键作用，如果K值太大，LLE不能体现局部特性。使得LLE算法趋向于PCA算法。反之取得太小，LLE便不能保持样本点在在低维空间中的拓扑结构。可使用  calc_k. 函数进行计算
• id: 逻辑变量，定义是否进行内存维度计算

Usage： calc_k(X, m, kmin=1, kmax=20, plotres=TRUE,parallel=FALSE, cpus=2, iLLE=FALSE)

• m: 输入数据的内在维度
• kmin: K最小值
• kmax: K最大值
• plotres：是否plot结果
• parallel： 是否使用并行计算

示例代码

> remove(list = ls())
> if (require(lle) == FALSE)
+ {
+    install.packages("lle")
+ }
>
> test <- iris[,1:4]
> le <- lle(test,5,20,id=TRUE)
finding neighbours
calculating weights
intrinsic dim: mean=3.96, mode=4
computing coordinates
> table(le$id)

  3   4
  6 144 

从上面的结果发现，输入数据的内在维度为2，再通过calc_k计算最合适的K值  

> k <- calc_k(test,2,kmin = 1,kmax = dim(test)[1])
snowfall 1.84-6.1 initialized: sequential execution, one CPU.

如下图，选择K值：50

根据计算优化的参数，重新进行数据计算

> le <- lle(test,2,50)
finding neighbours
calculating weights
computing coordinates
> newSet <- cbind(iris,as.data.frame(le$Y))
> head(newSet)
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species         V1        V2
1          5.1         3.5          1.4         0.2  setosa  0.5703337 -1.345773
2          4.9         3.0          1.4         0.2  setosa -0.7795944 -1.236492
3          4.7         3.2          1.3         0.2  setosa -0.8186908 -1.311557
4          4.6         3.1          1.5         0.2  setosa -1.2211154 -1.217567
5          5.0         3.6          1.4         0.2  setosa  0.5488266 -1.365494
6          5.4         3.9          1.7         0.4  setosa  1.9528668 -1.289062

结果图例显示

library(rgl)
plot_lle(le$Y,test)