动态规划入门——数字三角形（Java）

动态规划的概念对于新手来说枯燥难懂，就算看懂了，做题的时候依旧抓耳挠腮的毫无头绪，这些比较难理解的算法，还是需要根据例子来一步步学习和理解，从而熟练掌握，下面，咱们就通过一个简单的小例子来学习动态规划：

数字三角形(POJ1163)

在上面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。

路径上的每一步都只能往左下或 右下走。只需要求出这个最大和即可，不必给出具体路径。 三角形的行数大于1小于等于100，数字为 0 - 99

输入格式：

5      //表示三角形的行数    接下来输入三角形

7

3   8

8   1   0

2   7   4   4

4   5   2   6   5

要求输出最大和

咱们来分析这道题：

1.需要有一个变量 n 来存储输入的行数

2.需要一个二维数组 a 来存储输入的数字三角形

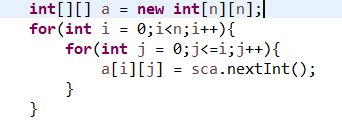
3.需要另一个同样大小的二维数组 b，用来存储到每一层的每一个数的最短路径，

例如：

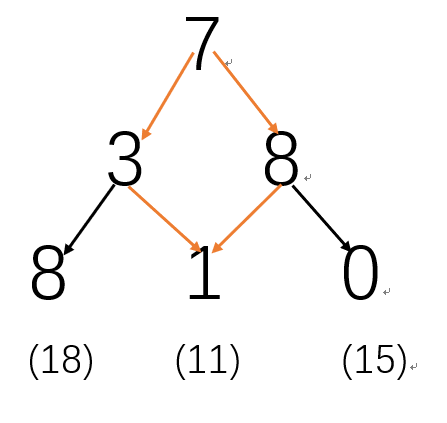
到三角形的第三层，有两条路会经过1，

由于7+3=10<7+8=15，所以b数组的1的位置存储的是最短路径7—>3—>1等于11，

而在最两边的，就直接累加就ok了，7+3+8=18，7+8+0=15

这也是这个程序的核心部分，代码如下：

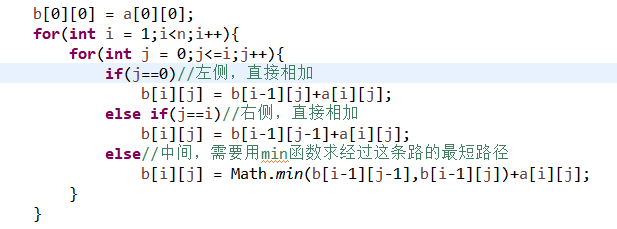
因为第一层跟a数组的第一层相同，所以i从1开始循环

然后遍历最后一层，求出最小值就ok啦

b数组最后的值

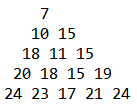
完整代码如下：

import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
		Scanner sca = new Scanner(System.in);
		int n = sca.nextInt();
		int[][] a = new int[n][n];
		int[][] b = new int[n][n];
		int min;
		for(int i = 0;i<n;i++){
			for(int j = 0;j<=i;j++){
				a[i][j] = sca.nextInt();
			}
		}

		b[0][0] = a[0][0];
		for(int i = 1;i<n;i++){
			for(int j = 0;j<=i;j++){
				if(j==0)//左侧，直接相加
					b[i][j] = b[i-1][j]+a[i][j];
				else if(j==i)//右侧，直接相加
					b[i][j] = b[i-1][j-1]+a[i][j];
				else//中间，需要用min函数求经过这条路的最短路径
					b[i][j] = Math.min(b[i-1][j-1],b[i-1][j])+a[i][j];
			}
		}

		min = b[n-1][0];
		for(int i = 1;i<b[n-1].length;i++){
			if(b[n-1][i]<min)
				min = b[n-1][i];
		}
		System.out.println(min);
	}
}

　　

总结一下动态规划的解题思路：

1，将原问题分解为简单的子问题，子问题求出来之后，原问题也就很容易得到了

2，确定状态转移方程

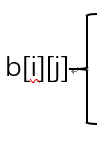
这道题的状态转移方程：

动态规划一般可分为线性动规，区域动规，树形动规，背包动规四类。

举例：

线性动规：拦截导弹，合唱队形，挖地雷，建学校，剑客决斗等；

区域动规：石子合并， 加分二叉树，统计单词个数，炮兵布阵等；

树形动规：贪吃的九头龙，二分查找树，聚会的欢乐，数字三角形等；

背包问题：01背包问题，完全背包问题，分组背包问题，二维背包，装箱问题，挤牛奶（同济ACM第1132题）等；

应用实例：

最短路径问题 ，项目管理，网络流优化等；

以上例子，每类挑选一题或两题练习即可

 

 

 

所有的算法都需要多加练习，应用起来才能得心应手，希望我的这篇博客能给各位爱学习的同伴们带去一些收获，我也是新手，大家共同努力，加油！