leetcode279

动态规划

public class Solution
    {
        public int NumSquares(int n)
        {
            var list = new List<int>();
            list.Add();
            for (int i = ; i <= n; i++)
            {
                list.Add(i);//每一个数字，初始化为全部由1构成
            }
            for (int i = ; i <= n; i++)
            {
                for (int j = ; j * j <= i; j++)
                {
                    var x = list[i];//当前值的构成数量，由全部是1来构成
                    var s = i - j * j;//减去一个平方数后的余数
                    var t = list[s];//余数值的构成数量
                    var y = t + ;//因为减过j*j，因此用余数的构成数量+1，相当于计算原值的构成数量

                    list[i] = Math.Min(x, y);
                }
            }
            return list[n];
        }
    }

补充一个python的实现，在leetcode上会TLE，经查询发现在讨论区中也有其他的人遇到了相同的TLE问题。

应该是对python语言的判断机制有问题，这种“平台语言杀”的问题出现过多次了。

 class Solution:
     def numSquares(self, n: int) -> int:
         dp = [] * (n + )
         #初始化，所有的数字都由''组成，dp中每个元素值为组成的数量
         for i in range(,n+):
             dp[i] = i
         for i in range(,n+):
             for j in range(,int(i**0.5)+):
                 res = i - j * j#减去一个完全平方数后的剩余值
                 dp[i] = min(dp[i],dp[res] + )
         return dp[n]

经过修改可以AC了，但是效率是比较低的：

 class Solution:
     def numSquares(self, n: int) -> int:
         dp = list(range(n+1))
         for i in range(,n+):
             for j in range(,int(i**0.5)+):
                 res = i - j * j#减去一个完全平方数后的剩余值
                 dp[i] = min(dp[i],dp[res] + )
         return dp[n]

既然python不能用dp方法提交，那就再提供一种别的思路，使用广度优先遍历(BFS)：

 class Solution:
     def numSquares(self, n: int) -> int:
         power = set()
         base =
         #生成符合条件的所有完全平方数，存储在power集合中
         while base*base <= n:
             curnum = base*base
             if curnum == n:
                 return
             power.add(curnum)
             base +=
         #level为返回值，表示最少的完全平方数的数量
         level =
         #初始目标设置为n
         target = {n}
         #判断条件target不为空
         while len(target) > :
             cur = set()
             #在目标集合中循环，获得一个值
             for i in target:
                 #在完全平方数集合中循环，获得一个值
                 for e in power:
                     #目标值 - 某个完全平方数 的差值，也是完全平方数
                     if i-e in power:
                         #返回 当前level +
                         return level+
                     #目标值 - 某个完全平方数 的差值，不是完全平方数，且大于0
                     if i-e > :
                         #将这个差值存储在‘下一层’
                         cur.add(i-e)
             #用下一层的值更新target
             target = cur
             #层级+
             level += 

以n=15为例，其计算流程如下：

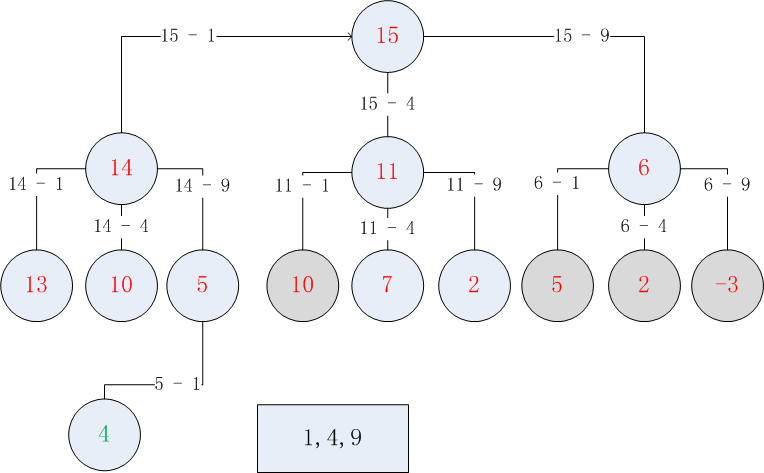
先计算小于等于15的值中，所有的完全平方数，如上图矩形区域所示(1,4,9)三个数值。

第一层的target中的值是：(15)，用15分别减去power中的数值，得到第二层；

第二层的target中的值是：(14,11,6)，三个数字都不在target集合中，因此继续计算第三层，用这三个数字分别减去power中的数值，得到第三层；

第三层的target中的值是：(13, 10, 5, 10, 7, 2, 5, 2, -3)，其中10，5，2出现了重复，使用set会自动去重，而-3 小于0，也会被过滤掉，

最终得到第三层的数值为：(13,10,5,7,2)，这五个数字都不在power中，因此继续用这5个数字计算第四层：

当计算5时，可得到 5 - 1 = 4，而4在power中，因此结束循环。此时节点5所在的“树的高度”为3(根结点从1开始计算)，因此level + 1 等于4。

最终返回4，即为所求，最终的完全平方数的组合是由线上的被减的值和叶子节点的值组成，即：[1,9,1,4]。