支持向量机(SVM)的推导(线性SVM、软间隔SVM、Kernel Trick)

线性可分支持向量机

给定线性可分的训练数据集，通过间隔最大化或等价地求解相应的凸二次规划问题学习到的分离超平面为
\[w^{\ast }x+b^{\ast }=0\]
以及相应的决策函数
\[f\left( x\right) =sign\left(w^{\ast }x+b^{\ast } \right)\]
称为线性可分支持向量机

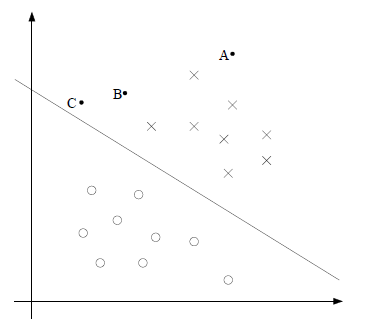
如上图所示，o和x分别代表正例和反例，此时的训练集是线性可分的，这时有许多直线能将两类数据正确划分，线性可分的SVM对应着能将两类数据正确划分且间隔最大的直线。

函数间隔和几何间隔

函数间隔

对于给定的训练集和超平面\((w,b)\)，定义超平面\((w,b)\)的函数间隔为：
\[\widehat\gamma_{i}=y_{i}(wx_{i}+b)\]

超平面\((w,b)\)关于训练集T的函数间隔最小值为：
\[\widehat\gamma=\min\limits_{i=1,\ldots,m}\widehat\gamma_{i}\]
函数间隔可表示分类预测的正确性及确信度，但是成比例改变\(w\)和\(b\)，例如将它们变为\(2w\)和\(2b\)，超平面并没有改变，但是函数间隔却变为了原来的2倍，因此可以对分离超平面的法向量\(w\)加某些约束，如规范化使\(\left\| w\right\|=1\)，这时函数间隔就成为了几何间隔。

几何间隔

对于给定的训练集T和超平面\((w,b)\)，定义超平面\((w,b)\)关于样本点\((x_{i},y_{i})\)的几何间隔为：
\[\gamma_{i}=y_{i}(\frac{w}{\left\|w\right\|}x_{i}+\frac{b}{\left\|w\right\|})\]

上述的几何间隔通过距离公式也可以计算出来。
定义超平面\((w,b)\)关于训练集T的几何间隔为超平面\((w,b)\)关于T中所有样本点的几何间隔的最小值：
\[\gamma=\min\limits_{i=1,\ldots,m}\gamma_i\]
从函数间隔和几何间隔的定义中可以看出，函数间隔与几何间隔有如下关系：
\[\gamma=\frac{\widehat\gamma}{\left\|w\right\|}\]

间隔最大化

SVM的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。
现在首先假设数据集线性可分，那么这个问题可以表述为下面的约束最优化问题：
\[\max\limits_{w,b}\quad\gamma\]
\[s.t.\quad y_i(wx_i+b)\geq\gamma\]
\[\left\|w\right\|=1\]

考虑函数间隔与几何间隔的关系，上式可以改写为：
\[\max\limits_{w,b}\quad\frac{\widehat\gamma}{\left\|w\right\|}\]
\[s.t.\quad y_{i}(wx_{i}+b)\geq\widehat\gamma\]

因为将\(w\)和\(b\)按比例改变对上述最优化问题的约束没有影响，对目标函数的优化也没有影响，因此就可以取\(\widehat\gamma=1\)，代入上面的最优化问题可以得：
\[\min\limits_{w,b}\quad\frac{1}{2}\left\|w\right\|^{2}\]
\[s.t.\quad y_{i}(wx_{i}+b)\geq1,\ i=1,\ldots,m\]
这就是线性可分支持向量机的最优化问题，这是一个凸二次规划问题。

对偶算法

对前面提出的最优化问题构建拉格朗日函数，得到：
\[L(w,b,\alpha)= \frac{1}{2}\left\|w\right\|^{2}-\sum\limits_{i=1}^{m}\alpha_{i}y_{i}(wx_{i}+b)+\sum\limits_{i=1}^{m}\alpha_{i}\]
首先需要最小化拉格朗日函数。
\[\min L(w,b,\alpha)\]
将拉格朗日函数\(L(w,b,\alpha)\)分别对\(w\)和\(b\)求偏导，得：
\[\nabla_{w}L(w,b,\alpha)=w-\sum\limits_{i=1}^{m}\alpha_{i}y_{i}x_{i}=0\]
\[\nabla_{b}L(w,b,\alpha)=-\sum\limits_{i=1}^{m}\alpha_iy_i=0\]
得到：
\[w=\sum\limits_{i=1}^{m}\alpha_{i}y_{i}x_{i}\]
\[\sum\limits_{i=1}^{m}\alpha_iy_i=0\]
代入到拉格朗日函数得：
\[L(w,b,\alpha)=-\frac{1}{2}\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}+\sum\limits_{i=1}^{m}\alpha_{i}\]
即：
\[\min L(w,b,\alpha)=-\frac{1}{2}\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}+\sum\limits_{i=1}^{m}\alpha_{i}\]
然后求\(\min L(w,b,\alpha)\)对\(\alpha\)的极大，即得对偶问题：
\[\max\limits_{\alpha}-\frac{1}{2}\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}+\sum\limits_{i=1}^{m}\alpha_{i}\]
\[s.t.\quad \sum\limits_{i=1}^{m}\alpha_{i}y_{i}=0\]
\[\quad\quad\quad\quad\quad\quad\quad \alpha_{i}\geq0, i=1,2,\ldots,m\]
将上式的目标函数由求极大转为求极小，即得：
\[\min\limits_{\alpha}\frac{1}{2}\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}-\sum\limits_{i=1}^{m}\alpha_{i}\]
\[s.t.\quad \sum\limits_{i=1}^{m}\alpha_{i}y_{i}=0\]
\[\quad\quad\quad\quad\quad\quad\quad \alpha_{i}\geq0, i=1,2,\ldots,m\]
得到最优化的解为：
\[w^{*}=\sum\limits_{i=1}^{m}\alpha_{i}^{*}y_{i}x_{i}\]
\[b^{*}=y_{j}-\sum\limits_{i=1}^{m}\alpha_{i}^{*}y_{i}x_{i}^{T}x_{j}\]
由上面两式可得，\(w^{*}\)和\(b^{*}\)只依赖于训练数据中对应于\(\alpha^{*}>0\)的样本点，将这些样本点成为支持向量。
根据KKT条件可知，支持向量一定在间隔边界上：
\[\alpha^{*}(y_{i}(w^{*}x_{i}+b)-1)=0\]
对应于\(\alpha^{*}> 0\)的样本，有：
\[y_{i}(w^{*}x_{i}+b)-1=0\]
即样本点一定在间隔边界上，因此在预测的时候只需要使用支持向量就可以了。

Kernels

当遇到分类问题是非线性的时候，就可以使用非线性的SVM来求解，在求解过程中，kernel trick十分的重要。
非线性变换的问题不好解，所以采用一个非线性变换，将非线性问题变换为线性问题，通过解变换后的线性问题来求解原来的非线性问题。
设原空间为\(\chi\subseteq R^{2}\)，\(x=((x^{(1)},x^{(2)}))^{T}\)，新空间\(Z\subseteqR^{2}\)，\(z=(z^{(1)},z^{(2)})^{T}\)，定义原空间到新空间的变换为：
\[z=\phi(x)=((x^{(1)})^{2},(x^{(2)})^{2})\]
然后就可以用新空间的点来求解问题。

Kernel Function

设\(\chi\)是输入空间，又设\(H\)为特征空间，如果存在一个从\(\chi\)到\(H\)的映射：
\[\phi(x):\chi\rightarrow H\]
使得对于所用的\(x,z\subseteq\chi\)，函数\(K(x,z)\)满足条件：
\[K(x,z)=\phi(x)^{T}\phi(z)\]
则称\(K(x,z)\)为核函数，\(\phi(x)\)为映射函数。

Kernel Trick

kernel trick是想法是在学习和预测过程中只定义核函数\(K(x,z)\)，而不显示地定义映射函数\(\phi(x)\)。
初学SVM时容易对kernel有一个误解：以为是kernel使低维空间的点映射到高维空间后实现了线性可分。
但是实际中kernel其实是帮忙省去在高维空间里进行繁琐计算，它甚至可以解决无限维无法计算的问题。
下面给一个例子：

定义一个二次变换：
\[\phi_{2}(x)=(1,x_{1},x_{2},\ldots,x_{d},x_{1}^{2},x_{1}x_{2},\ldots,x_{1}x_{d},x_{2}x_{1},x_{2}^{2},\ldots,x_{2}x_{d},\ldots,x_{d}^{2})\]
上式为了简化同时包含了\(x_{1}x_{2}\)和\(x_{2}x_{1}\)
可以求得一个核函数：
\[\phi_{2}(x)^{T}\phi_{2}(z)=1+x^{T}z+(x^{T}z)(x^{T}z)\]
这样在计算的时候代入核函数求内积比直接用变换后的向量点乘直接求的速度快多了。复杂度也从\(o(d^{2})\)降到了\(o(d)\)

所以不能说是kernel trick完成了低维到高维的变换，kernel trick只是为这种变换之后的计算服务的一个技巧，真正的变换在定义\(\phi(x)\)的时候已经完成了。

常用的kernel function

• 多项式核函数(polynomial kernel function)
  \[K(x,z)=(1+x^{T}z)^{p}\]
• 高斯核函数(Gaussion kernel function)
  \[K(x,z)=\exp(-\frac{\left\|x-z\right\|^{2}}{2\sigma^{2}})\]
  高斯核函数也叫径向基核函数（RBF）
  在使用了核函数后，最后预测函数变为：
  \[f(x)=sign(\sum\limits_{i=1}^{N^{s}}\alpha_{i}^{*}y_{i}K(x_{i},x)+b^{*})\]

软间隔支持向量机(soft-margin)

线性可分支持向量机的学习方法对线性不可分的训练数据是不适用的。线性不可分意味着某些样本点\((x_{i},y_{i})\)不能满足函数间隔大于等于1的条件，那么可以引入一个松弛变量\(\xi_{i}\geq0\)，这样约束条件就变为了：
\[y_{i}(wx_{i}+b)\geq1-\xi_{i}\]
这样线性不可分的SVM学习问题变成了如下的问题：
\[\min\limits_{w,b,\xi} \frac{1}{2}\left\|w\right\|^{2}+C\sum\limits_{i=1}^{m}\xi_{i}\]
\[s.t. \quad y_{i}(wx_{i}+b)\geq1-\xi_{i}, i=1,\ldots,m\]
\[\xi_{i}\geq0,i=1,\ldots,m\]
这样拉格朗日函数变为：
\[L(w,b,\xi,\alpha,\mu)=\frac{1}{2}\left|w\right\|^{2}+C\sum\limits_{i=1}^{m}\xi_{i}-\sum\limits_{i}^{m}\alpha_{i}(y_{i}(wx_{i}+b)-1+\xi_{i})-\sum\limits_{i=1}^{m}\mu_{i}\xi_{i}\]
分别对\(w、b、\xi\)求偏导，最后得到的对偶问题为：
\[\min\limits_{\alpha}\frac{1}{2}\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}-\sum\limits_{i=1}^{m}\alpha_{i}\]
\[s.t.\quad \sum\limits_{i=1}^{m}\alpha_{i}y_{i}=0\]
\[\quad\quad\quad\quad\quad\quad\quad 0\leq\alpha_{i}\leq C, i=1,2,\ldots,m\]

软间隔最大化时的支持向量

根据KKT条件有\(\alpha_{i}^{*}(y_{i}(wx_{i}+b)-1+\xi_{i})=0\)和\(\mu_{i}\xi_{i}=0\)，又\(\mu_{i}=C-\alpha_{i}\)所以有：

• 如果\(\alpha=0\)那么\(y_{i}(wx_{i}+b)\geq1\)，此时样本在间隔边界或者被正确分类。
• 如果\(0<\alpha<C\)，那么\(\xi_{i}=0\)，\(y_{i}(wx_{i}+b)=1\)，点在间隔边界上。
• 如果\(\alpha=C\)
  1. 若\(0<\xi_{i}<0\)，那么点被分类正确，且在超平面和间隔边界之间。
  2. 若\(\xi_{i}=1\)，那么点在超平面上，无法分类。
  3. 若\(\xi_{i}>1\)，那么点位于超平面误分类的一侧。

SMO算法

SMO算法用于快速实现SVM，包含两个部分：求解两个变量二次规划的解析方法和选择变量的启发式方法。
假设固定住\(\alpha_3,\ldots,\alpha_m\)，那么优化问题就依赖于\(\alpha_{1}、\alpha_{2}\)，此时可以得到：
\[\alpha_{1}y_{1}+\alpha_{2}y_{2}=-\sum\limits_{i=3}^{m}\alpha_{i}y{i}=\zeta\]
可得到\(\alpha_{1}、\alpha_{2}\)的约束图如下：

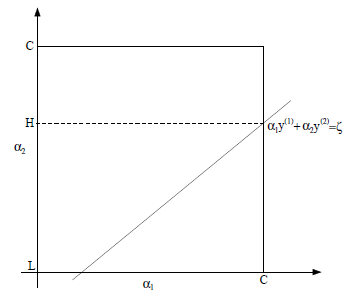
因为\(y_i\in[-1,1]\)，因此上述约束条件可以转化为：
\[\alpha_{1}=(\zeta-\alpha_{2}y_{2})y_{1}\]
这样就可以求得\(\alpha_{2}\)
但是\(\alpha_{2}\)有限制条件，因此可能会被修剪，最终\(\alpha_{2}^{new}\)的取值为：
\[\alpha_{2}^{new}=\begin{cases}
H & if \quad\alpha_2^{new,unclipped}>H \\
\alpha_2^{new,unclipped} & if \quad L\leq\alpha_2^{new,unclipped}\leq H \\
L & if\quad \alpha_2^{new,unclipped}\leq L
\end{cases}\]
最后可以根据\(\alpha_{2}^{new}\)计算出\(\alpha_{1}^{new}\)。

变量选择方法

• SMO选择第一个变量的过程为外层循环，外层循环在训练样本中选取违反KKT条件最严重的样本点。
• SMO选择第二个变量的过程为内层循环，第二个变量选择的标准是希望能使\(\alpha_{2}\)有足够大的变化。

实现

最后我简单用python实现了下SVM，仓库地址为:SVM的实现