题目大意：在n*n的棋盘中，放置n个皇后（同一行、同一列、同一斜线，只有一个皇后）

这道题是一道非常经典的dfs模板题，同一行、同一列的判断不是很难，但同一斜线有一定的难度，下面给出关于斜线编号的解决方法

我们就先以4*4的棋盘为例

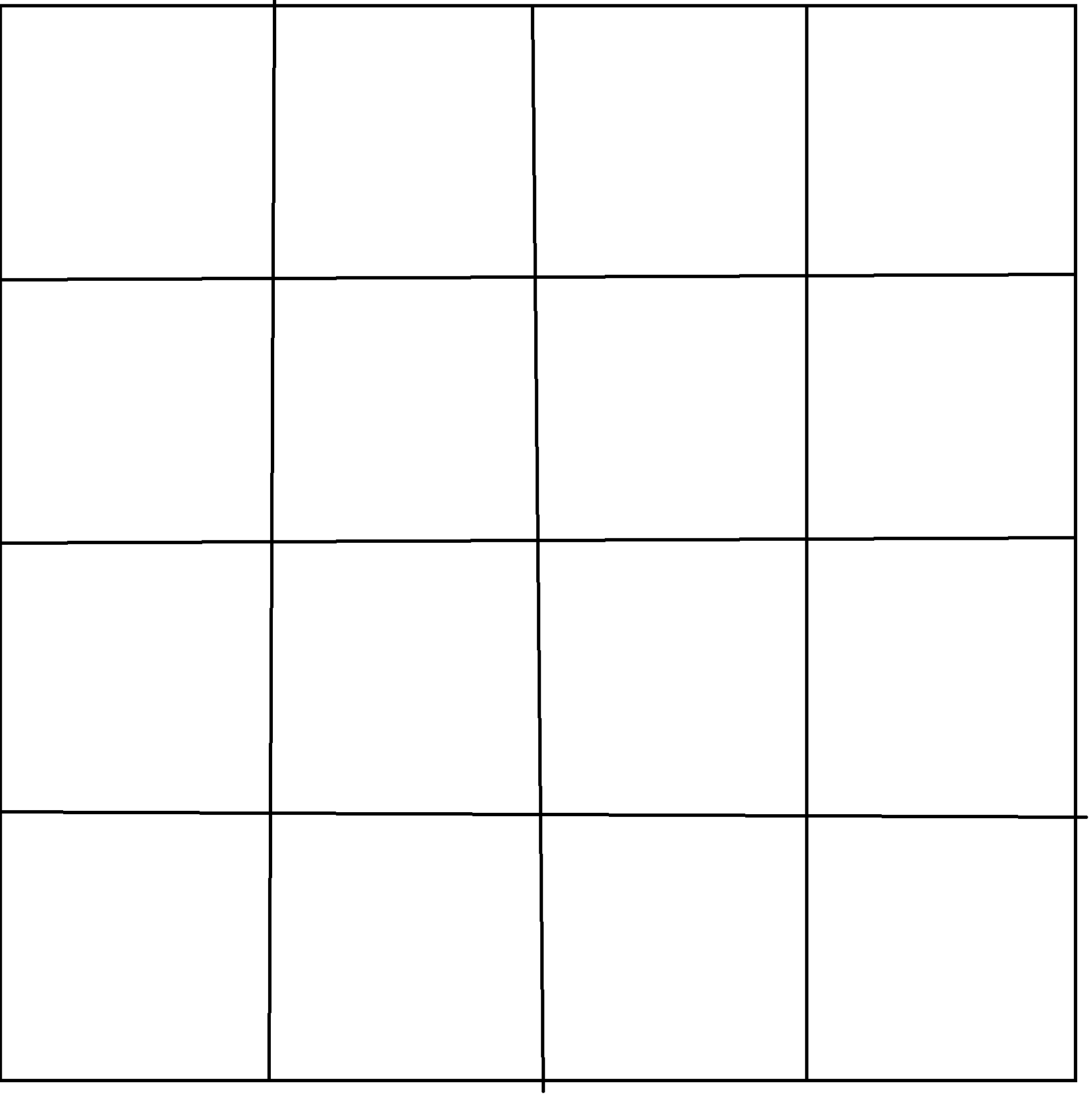
我们把被标红的这一条暂且称之为主对角线

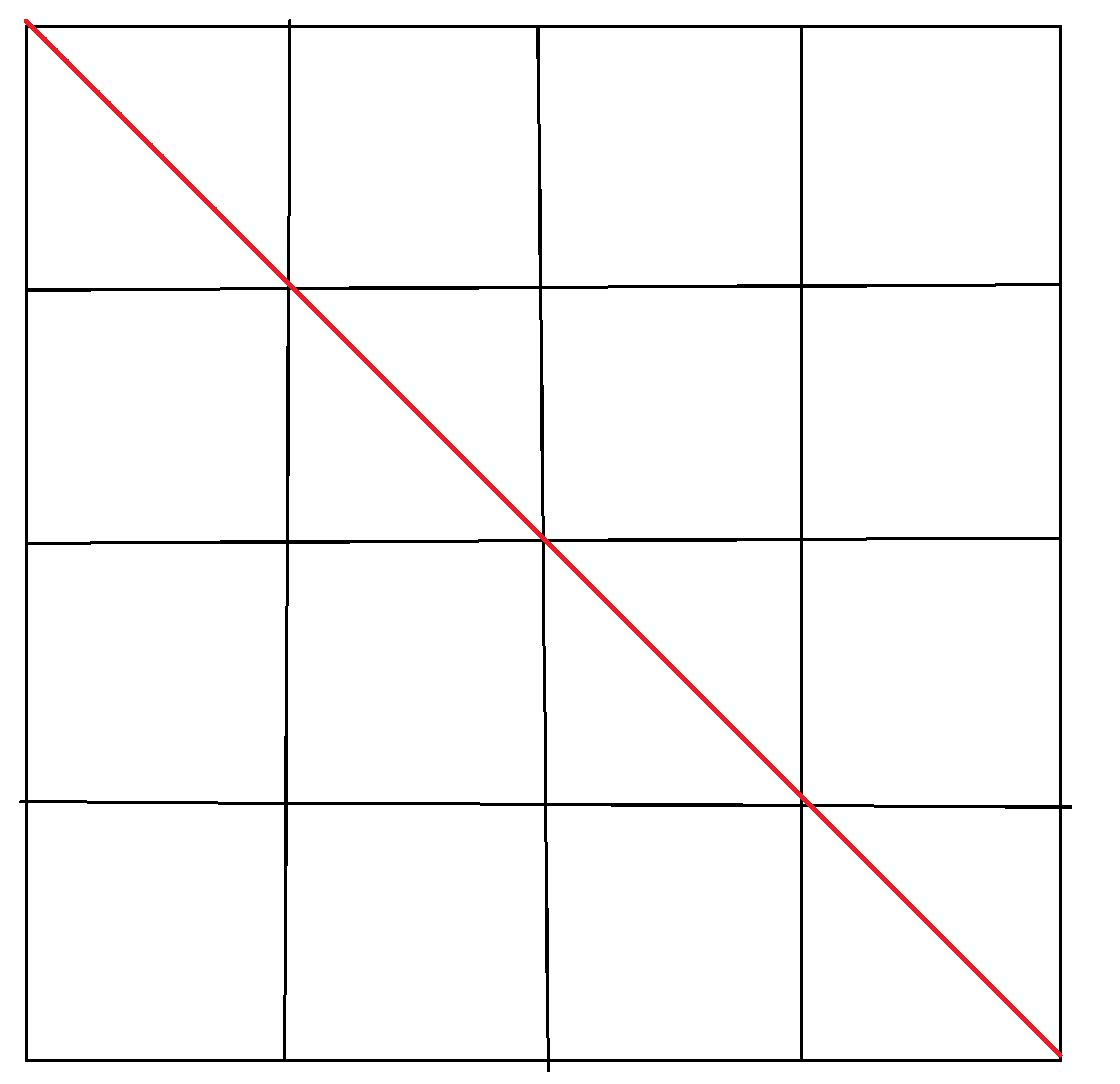
观察一下主对角线上的点坐标规律

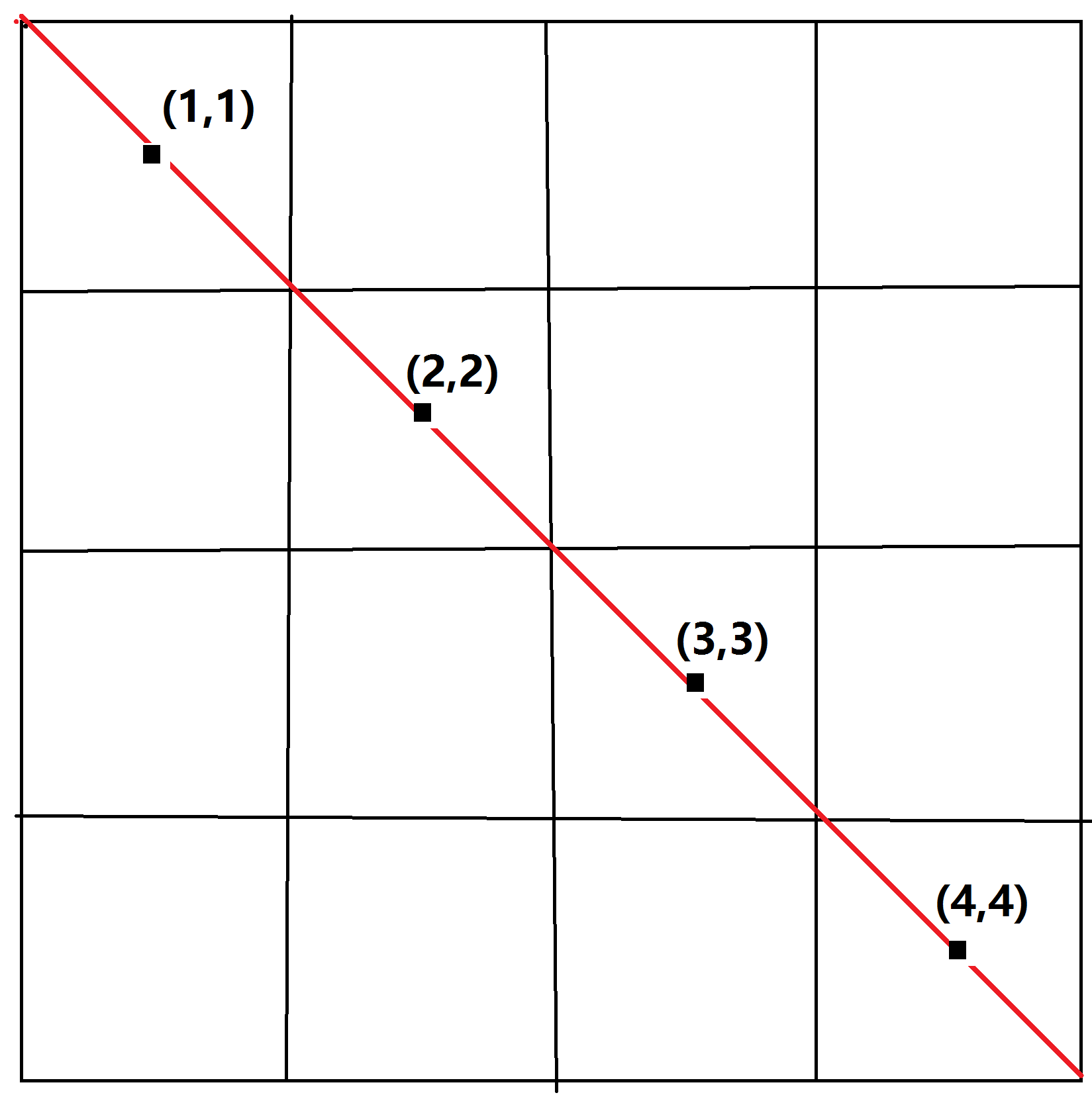
我们发现主对角线上的点的坐标（x，y）满足x==y

下面看看其他的斜线有怎样的性质

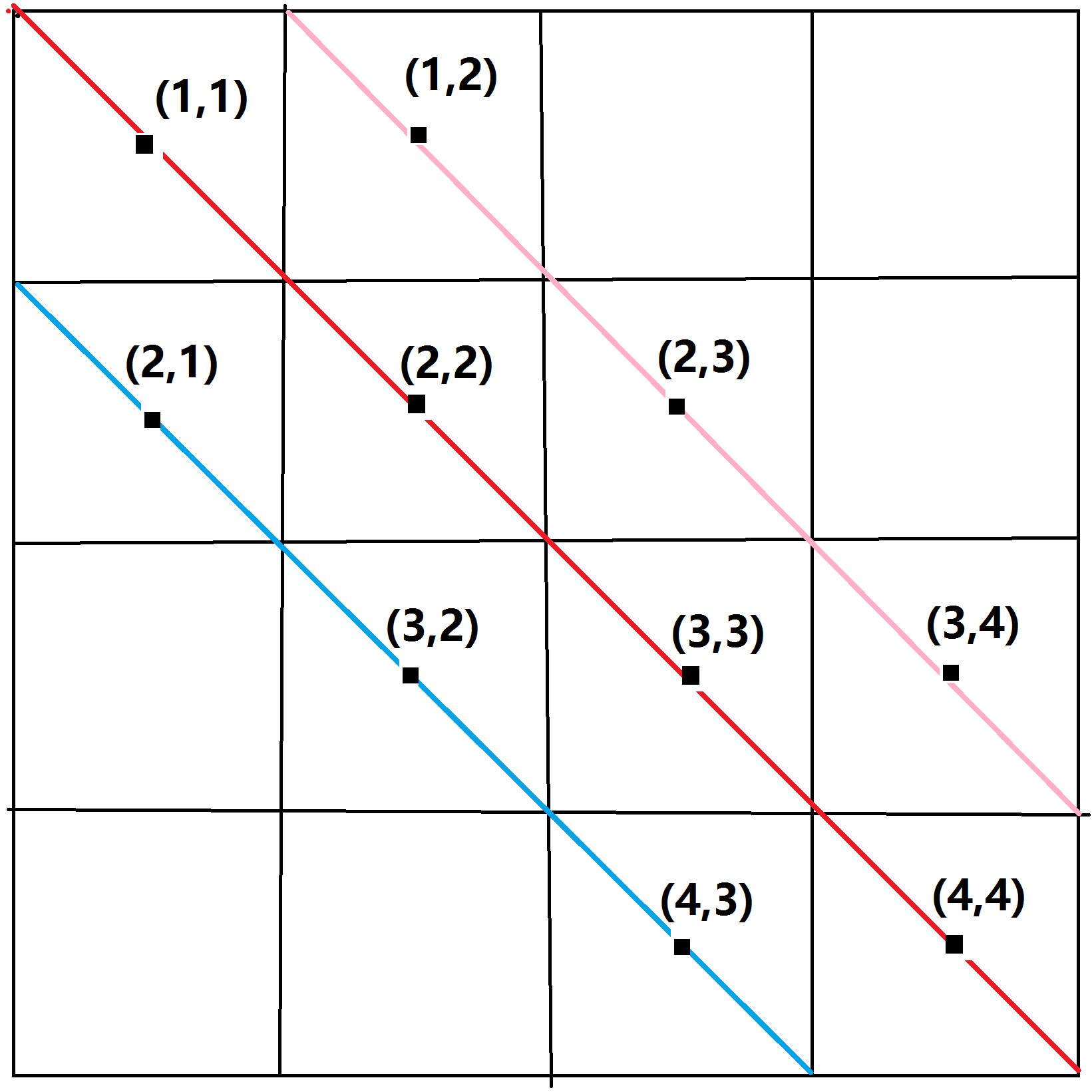
在蓝色这条斜线上的坐标（x,y）满足x-y==1

在粉色这条斜线上的坐标（x,y）满足x-y==-1

同样的，我们也可以吧主对角线的坐标（x,y）表示为x-y==0

所以可以用x-y来计算斜线的编号

x-y的值是从(-4+1)~(4-1)

但是数组下标（在c++）没有负数，所以我们把x-y+n当做数组下标，编号从1~（2*4-1）

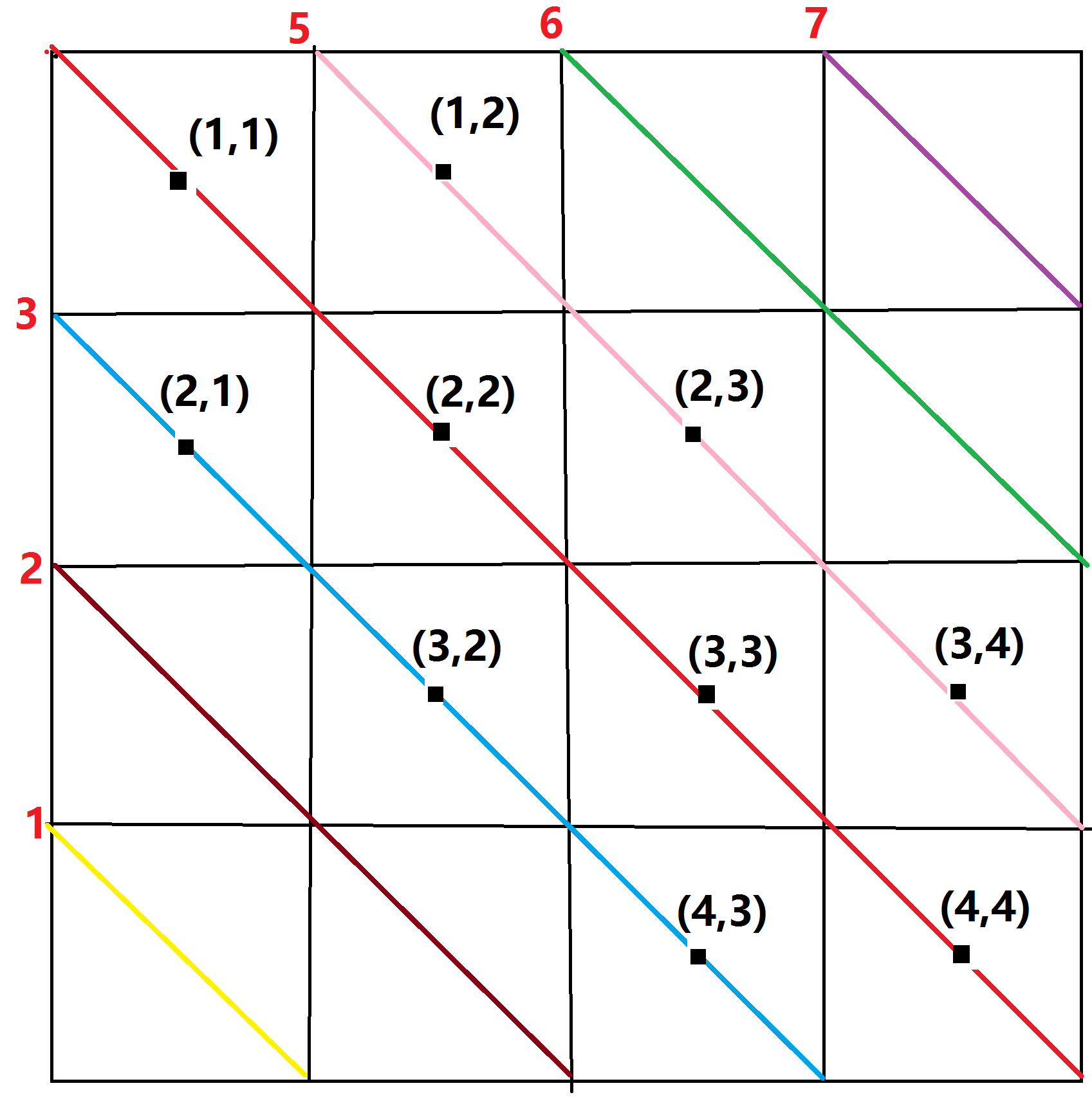
同样的，对于n*n的棋盘，共有2n+1条左斜线，我们可以把向左倾斜的斜线编号为（x-y+n）

下面来解决一下向右倾斜的斜线编号（还是以4*4的棋盘为例）

不难看出，在标红的这条向右倾斜的主对角线上点的坐标满足x+y==5

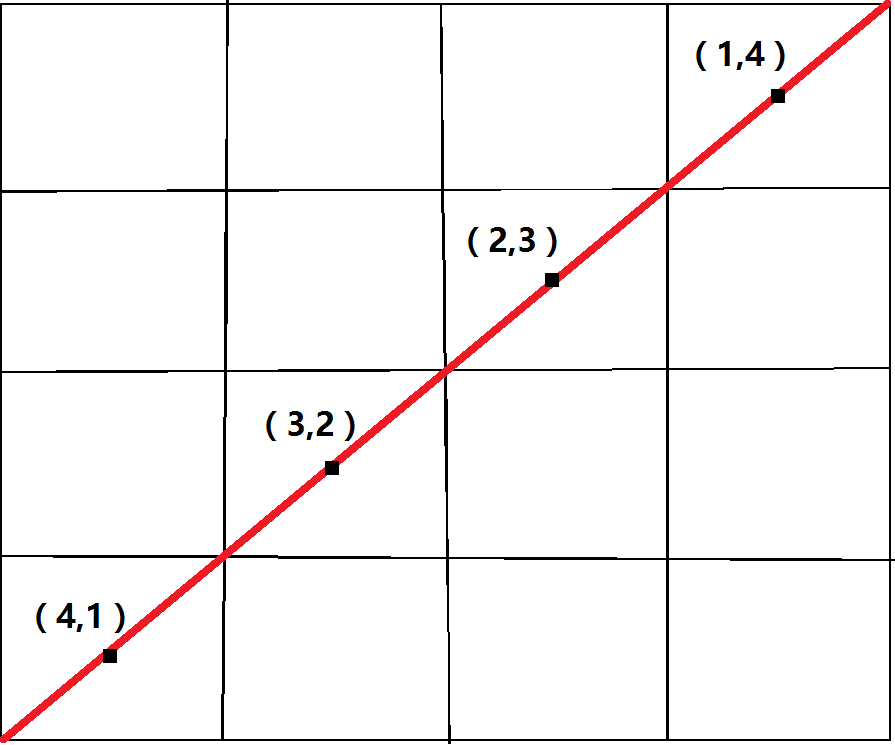
在粉色的这条斜线上x+y==4

在蓝色的这条斜线上x+y==6

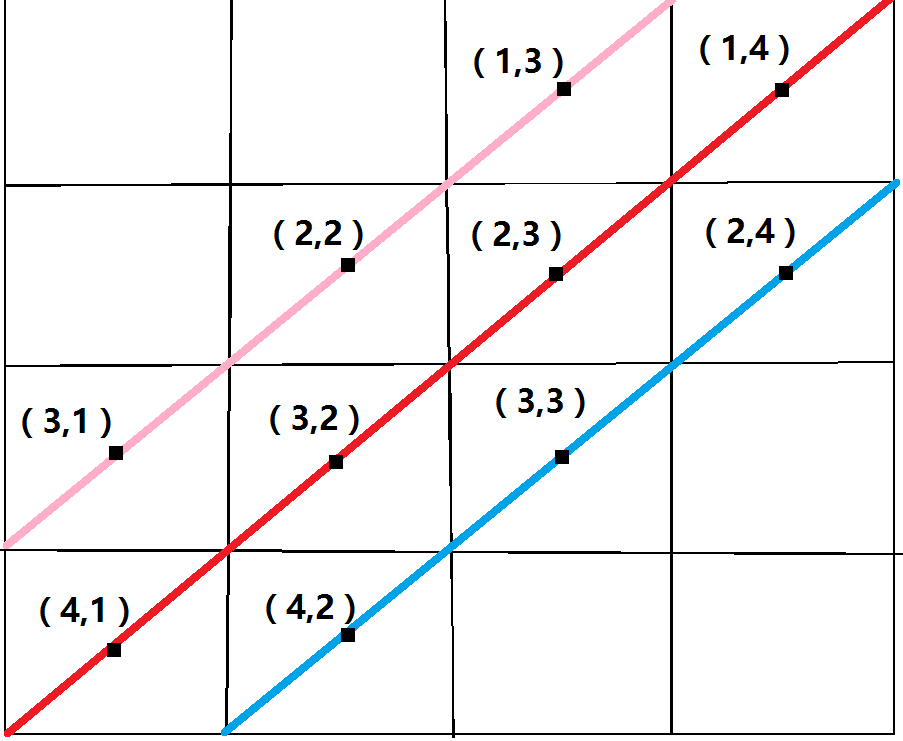
同样的，向右倾斜的斜线共有（2*4-1）条，按照x+y来编号，编号为2~8，因为我们普遍采用从1开始的数组下标

所以我们用（x+y-1）当做数组下标，范围是1~7

同样的，对于n*n的棋盘，共有2n+1条右斜线，我们可以把向右倾斜的斜线标号为（x+y-1）

n皇后问题——关于斜线的编号的更多相关文章

  1. N皇后问题【递归求解】

    n皇后问题:输入整数n, 要求n个国际象棋的皇后,摆在n*n的棋盘上,互相不能攻击,输出全部方案. 输入一个正整数N,则程序输出N皇后问题的全部摆法.输出结果里的每一行都代表一种摆法.行里的第i个数字 ...

  2. 带你轻而易举的学习python——八皇后问题

    首先我们来看一下这个著名的八皇后问题 八皇后问题:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行.同一列或同一斜线上,问有多少种摆法. 在这个问题提出之后人们又将 ...

  3. n皇后问题_回溯法

    具体问题如下图 先看一下4*4的回溯过程 程序结束条件: 一组解:设标志,找到一解后更改标志,以标志做为结束循环的条件. 所有解:k=0 判断约束函数判断第k个后能不能放在x[k]处 两个皇后不能放在 ...

  4. 蓝桥--2n皇后问题（递归）--搬运+整理+注释

    N皇后问题: #include <iostream> #include <cmath> using namespace std; int N; ];//用来存放算好的皇后位置. ...

  5. 8皇后问题SQL求解（回溯算法）

    问题 八皇后问题是一个古老而著名的问题,是回溯算法的典型例题.该问题是十九世纪著名的数学家高斯1850年提出:在8X8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行.同一 ...

  6. C#数据结构与算法系列（十四）：递归——八皇后问题（回溯算法）

    1.介绍 八皇后问题,是一个古老而著名的问题,是回溯算法的经典案例,该问题是国际西洋棋棋手马克斯.贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即 任意两个皇后都不能处 ...

  7. Java 内功修炼 之 数据结构与算法（一）

    一.基本认识 1.数据结构与算法的关系? (1)数据结构(data structure): 数据结构指的是 数据与数据 之间的结构关系.比如:数组.队列.哈希.树 等结构. (2)算法: 算法指的是 ...

  8. 经典算法问题的java实现 (二)

    原文地址: http://liuqing-2010-07.iteye.com/blog/1403190   1.数值转换(System Conversion) 1.1 r进制数   数N的r进制可以表 ...

  9. HLOJ1361 Walking on the Grid II 矩阵快速幂

    题目分析: 就当是一次记录吧,2013年绍兴市市赛的一题,重现赛当时我想递推可能是矩阵快速幂吧,但是这个递推公式真没推出来(赛后猛如虎系列),这题和第一题有联系又有区别,第一题的递推很简单,dp[i] ...

随机推荐

  1. dubbo+spring_maven 遇到的问题 Error creating bean with name '***': Instantiation of bean failed;

    Exception in thread "main" org.springframework.beans.factory.BeanCreationException: Error ...

  2. 高仿QQ、微信效果的图片浏览器（支持原图和缩略图、多种手势、CocoaPods）

    感谢原文作者的分享 本文转载至 http://my.oschina.net/u/2406027/blog/735738 PYPhotoBrowser GitHub地址:https://github.c ...

  3. Abp之工作单元与事务

    环境:Abp1.2 疑问:没有调用工作单元的SaveChanges方法引起的事务提交时机的问题. 例如:有一个应用服务代码如下: public void CreatePhrase(PhraseCrea ...

  4. JavaSE 可变参数的方法重载

    /** * 可变参数的方法重载 */ class A { public void test(int a, int b) { System.out.println(a+", "+b) ...

  5. 在cmd启动一个win32程序,printf把信息输出到启运它的那个CMD窗口

    #define ProcessBasicInformation 0 typedef struct { DWORD ExitStatus; DWORD PebBaseAddress; DWORD Aff ...

  6. Nginx模块开发与架构解析(nginx安装、配置说明)

    第一章 研究nginx前的准备工作 Linux操作系统需要2.6及其以上的内核(支持epoll) 使用nginx的必备软件 Linux内核参数优化方案 安装nginx 控制nginx 第二章 ngin ...

  7. Tanya and Candies

    Tanya and Candies time limit per test 1 second memory limit per test 256 megabytes input standard in ...

  8. css的小知识

    ---恢复内容开始--- 1.当你发现在制作页面时出现滚动条就需要一个去除滚动条的属性 overflow:hidden:           overflow-x:hidden:水平超出隐藏 2.  ...

  9. Java远程连接redis, 报错 Connection refused: connect

    在今天的学习Redis中报错 Connection refused: connect 我总结了有三种情况: 1.远程服务器中的Redis没有开启. 2.远程连接地址出错,或者是端口出错. 3.远程服务 ...

  10. 编写函数求整形数组a中存储的m个不重复的整数的第k大的整数(其中m>=1,1<=k<=m)很简单的一个思路是酱紫的：管他辣么多干啥，上来一把排序然后直接得答案

    /** * @author:(LiberHome) * @date:Created in 2019/2/28 20:38 * @description: * @version:$ *//*编写函数求整 ...