【LeetCode数组#1二分法】二分查找、搜索插入、在排序数组中查找元素的第一个和最后一个位置

二分查找

题目

力扣704题目链接

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

• 你可以假设 nums 中的所有元素是不重复的。
• n 将在 [1, 10000]之间。
• nums 的每个元素都将在 [-9999, 9999]之间。

初见思路

虽然这套题有明确的考察点，但是我习惯拿到题先用最笨的办法实现一次，然后再改进算法

这题整体还是比较简单的，如果用常规的思路也很容易做出来

例如：遍历数组，找到符合条件的值，然后返回其下标，如果条件均不满足，则返回默认下标值（-1）

class Solution {
    public int search(int[] nums, int target) {
        int index = -1;
        for(int i = 0; i < nums.length; i++){
            if(nums[i] == target){
                index = i;
            }
        }
        return index;
    }
}

那么实际上，本题考察的主要是“查找”数组的过程

显然，遍历的方式对于二分法来说，是非常低效的，因此肯定是要用二分法来写的

常规思路

在升序数组nums中寻找目标值target，对于特定下标 i，比较nums[i]和target的大小

• 如果nums[i] = target，则下标 i 即为要寻找的下标;
• 如果nums[i] > target，则 target 只可能在下标 i 的左侧;
• 如果nums[i] < target，则target只可能在下标 i 的右侧。

基于上述事实，可以在有序数组中使用二分查找寻找目标值。【ps：如果数组是乱序，那么有你可能会找出多个值】

二分法的解题流程如下：

1、定义一个查找的范围，一般用left和right代表左右边界

2、在该范围内取中点middle，比较nums[mid]和target

3、根据比较结果进行返回或继续对某侧进行查找

解题模板

实际上二分法有两种写法，分别是左闭右闭和左闭右开【即是否包含边界点本身】，模板只记一种就行，另外的补充再说

c++版

class Solution {
public:
    int search(vector<int>& nums, int target) {
        //定义左右边界
        int left = 0;
        int right = nums.size() - 1;
        while(left <= right){
            //计算中间值
            int mid = (right - left)/2 + left;//定位mid值所在位置
            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] < target){
                //移动左边界
                left = mid + 1;
            }else if(nums[mid] > target){
                //移动右边界
                right = mid - 1;
            }
        }
        return -1;
    }
};

二刷问题

移动边界时，逻辑没有处理好。忘了要跳过mid

要移动左边界的话，移动的目标位置应该是当前mid的后一位

而移动左边界的话，目标位置应该是当前mid的前一位

Java版

class Solution {
    public int search(int[] nums, int target) {
        //①定义左右边界
        int left = 0, right = nums.length - 1;
        //②写一个条件循环*
        while (left <= right) {
            //计算区间的中点mid
            int mid = (right - left) / 2 + left;//用减是为了防止数据溢出，加left是为了定位到当前区间
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] > target) { //此时，target只能在区间中点的左半部分，因此右边界改变，变为左半部分的右边界
                right = mid - 1;
            } else if(nums[mid] < target) {//target只能在区间中点的右半部分，因此左边界改变，变为右半部分的左边界
                left = mid + 1;
            }
        }
        return -1;//找不到返回-1
    }
}

注释：

边界问题

在上述写法中有两处值得关注的边界，

一处是while的条件left <= right【什么时候要写<、什么时候写<=】，一处是边界改变时的mid - 1【什么时候写mid，什么时候写mid-1】

这两个边界问题都只取决于你决定采用哪种二分法的写法，在一开始我们就必须先确定要用左闭右闭还是左闭右开，然后后面再写的时候要贯彻执行，根据区间的定义去选择边界

以左闭右闭[left, right]为例

当忘了while里应该写<=还是<时，可以想一想一开始确定的区间

比如，如果我写left <= right，对于[left, right]来说是不是合法的呢？【[1,1]，1到1的区间且包含1，虽然只有一个元素但至少不非法】

显然还是可以这么写的，所以在左闭右闭时应该写left <= right

类似的，left <= right对于[left, right)则不合法【[1,1)，即包含1又不含1？】

那么mid呢？

假设目前你的nums[mid] > target，那么这个target一定不会出现在当前mid的右边区间了

所以下一步应该从左边区间再查找

这时候应该将当前的右边界调整到左边区间上来，并且需要排除掉当前的nums[mid]

因此下次查找的右边界的下标应该是right = mid - 1

如果不减1就相当于把一个不属于下次查找区间的数放到区间中了，对于区间来说是非法的，自然会出错

类似的，right = mid - 1对于[left, right)则不合法，因为[left, right)在下次查找中本来就不包含right，所以应该直接写right = mid【若nums[mid] < target，则[left, right)的left还是需要写成left = mid - 1，因为left在[left, right)中是被包括在内的】

Python版

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        while left <= right:
            mid = (right - left)//2 + left
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            else:
                right = mid - 1
        return -1

拓展练习

LeetCode35搜索插入位置

思路就是二分查找，这里还是选左闭右闭的方式去写

c++版

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        //定义左右边界
        int left = 0;
        int right = nums.size() - 1;
        while(left <= right){
            //计算mid
            int mid = (right - left)/2 + left;
            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] < target){
                //移动左边界
                left = mid + 1;
            }else if(nums[mid] > target){
                //移动右边界
                right = mid - 1;
            }
        }
        return right + 1;
    }
};

基本上还是按照二分查找的思路去写的，这里的关键是遍历完成之后的返回值

为什么是返回right + 1？

遍历完之后可以有以下几种情况：（都是没找到target的情况）

1、遍历完了还没结束说明并没有找到target

此时需要返回插入位置，因为跳出while循环了，此时的 left 肯定大于 right

  l↓ ↓r
[1,2,3,4]

  r↓ ↓l
[1,2,3,4]

此时，要插入的位置是2和3之间，因为r已经跑到小于l的位置，所以要加回来然后返回（即right + 1），这样target才能插到2和3之间

2、遍历到了右边界还没找到找到target

    l↓ ↓r
[1,2,3,4]

此时，需要插入的位置是right + 1（即数组末尾）

3、遍历到了左边界还没找到找到target

此时只能是 left 大于 right 才会发生的情况，因为缩右边界时，左边界是不变的，如果一直nums[mid] > target，那就会一直移动右边界，直到超过一直不动的left，循环结束，此时情况如下：

↓rl↓
  [1,2,3,4]

右边界已经指向数组外面，所以要加回来，加到l在的位置再插入target

即right + 1

因此，在while循环结束后返回right + 1可以处理多种情况

Java版

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while(left <= right){
            int mid = (right - left)/2 + left;
            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] < target){
                left = mid + 1;
            }else{
                right = mid - 1;
            }
        }
        //此处可以同时处理四种情况下的返回值
        //1、目标值等于数组中某一个元素  return middle;
        //2、目标值插入数组中的位置 [left, right]，return  right + 1
        //3、目标值在数组所有元素之后的情况 [left, right]，这是右闭区间，所以  return right + 1
        //4、目标值在数组所有元素之前  [0, -1]【没想通】
        return right+1;
    }
}

Python版

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums)-1
        while left <= right:
            mid = (right - left)//2 + left
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            else:
                right = mid - 1

        return right+1

LeetCode34在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8

输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6

输出：[-1,-1]

示例 3：

输入：nums = [], target = 0

输出：[-1,-1]

思路

从示例1来看，我们查找的元素可以是多个，然后需要返回的是多个数位于数组中的区间（暂且称为结果区间）

因此需要分别求结果区间的左边界和右边界

一种笨一点但比较有条理的方式是：使用二分法分别求出左边界和右边界，然后再根据条件判断

在此之前我们需要明确会出现的情况

情况1：target出现在数组范围的左边

nums = [5,7,7,8,8,10], target = 2

因为数组nums是进过排序的，因此2是在数组范围的左边

当然此时是不能从数组中找到terget的，因此要返回{-1,-1}

情况2：target出现在数组范围的右边

nums = [5,7,7,8,8,10], target = 16

同理，此时也无法再数组中找到target，因此要返回{-1,-1}

情况3：target在数组范围内

nums = [5,7,7,8,8,10], target = 8

因为nums是经过排序的整数数组，所以一旦target落在数组范围内，那必然会有匹配值

上面的情况返回值应该是{3,4}

下面来分别求左右边界

代码分析

寻找左右边界的代码实际上就是单独的二分法代码

但里面有一些需要注意的点，先看代码整体框架

class Solution {
private:
    int getRightBorder(vector<int>& nums, int target) {

    }
    int getLeftBorder(vector<int>& nums, int target) {

    }

public:
    vector<int> searchRange(vector<int>& nums, int target) {

    }
};

因为要单独求左边界和右边界，所以单独定义两个函数负责做这件事

函数定义如下

class Solution {
private:
    int getRightBorder(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        int rightBorder = -2;
        while(left <= right){
            int mid = (right - left)/2 + left;
            if(nums[mid] > target){
                right = mid - 1;
            }else{
                left = mid + 1;
                rightBorder = left;
            }
        }
        return rightBorder;
    }
    int getLeftBorder(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        int leftBorder = -2;
        while(left <= right){
            int mid = (right - left)/2 + left;
            if(nums[mid] >= target){
                right = mid - 1;
                leftBorder = right;
            }else{
                left = mid + 1;
            }
        }
        return leftBorder;
    }

public:
    vector<int> searchRange(vector<int>& nums, int target) {
    }
};

这里有几点需要注意的

1、左边界和求右边界的核心代码是一个逻辑

实际上，求左边界和求右边界的核心代码是一个逻辑，都是简单的二分法

但是，因为要求的是左右边界，所以加入了一些条件对查找范围进行了控制

2、为什么左右边界的初始值都是-2？

因为这是一个特殊值，方便在没找到的情况下返回题目要求的{-1,-1}

3、为什么求右边界时，循环中的条件是nums[mid] > target，而求左边界时是nums[mid] >= target？

在求解右边界和左边界时，循环中的条件不同的原因是为了确保获取到正确的边界值。

• 求解右边界时（getRightBorder函数），我们需要找到第一个大于目标值的元素位置。因此，当 nums[middle] > target 时，我们将 right 更新为 middle - 1，继续在左半部分查找（目标值在mid的左边）。而当 nums[middle] == target 时，我们需要更新左边界，因为目标值可能出现在右半部分。所以我们将 left 更新为 middle + 1，同时记录当前的 left 值作为右边界的候选位置。
• 求解左边界时（getLeftBorder函数），我们需要找到第一个大于或等于目标值的元素位置。因此，当 nums[middle] >= target 时，我们将 right 更新为 middle - 1，继续在左半部分查找。同时，我们将当前的 right 值记录为左边界的候选位置。而当 nums[middle] < target 时，我们将 left 更新为 middle + 1，继续在右半部分查找。

通过这样的条件设置，最终得到的左边界和右边界位置可以保证是符合要求的。在最坏情况下，左边界和右边界都是在数组的边界位置，即左边界是 -1，右边界是 nums.size()。在函数的返回值中，如果左边界和右边界的差值大于 1，则说明存在目标值，并且返回的结果为目标值的范围（左边界加 1，右边界减 1）；如果差值为 1，则说明只有一个目标值，返回的结果为 -1, -1；如果左边界和右边界都是边界值，则说明目标值不存在，返回的结果为 -1, -1。

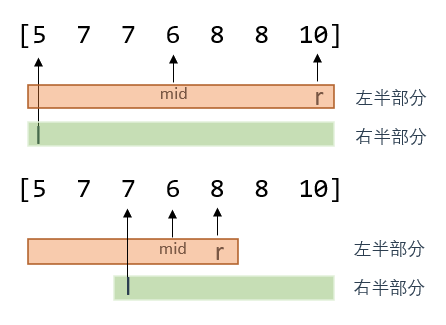
4、为什么使用left作为右边界的更新值，使用right作为左边界的更新值？

这个问题实际上在问题3中已经解释了

这里需要画个图：

完整代码

注意点：

1、求左右边界的函数核心实现是一样的，只是记录左右边界的位置不同

2、左右边界变量值初始化为-2

3、求左边界时记得right指针更新的条件是大于等于

class Solution {
private:
    int getRightBorder(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        int rightBorder = -2;
        while(left <= right){
            int mid = (right - left)/2 + left;
            if(nums[mid] > target){
                right = mid - 1;
            }else{
                left = mid + 1;
                rightBorder = left;
            }
        }
        return rightBorder;
    }
    int getLeftBorder(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        int leftBorder = -2;
        while(left <= right){
            int mid = (right - left)/2 + left;
            if(nums[mid] >= target){
                right = mid - 1;
                leftBorder = right;
            }else{
                left = mid + 1;
            }
        }
        return leftBorder;
    }

public:
    vector<int> searchRange(vector<int>& nums, int target) {
        //计算左右边界
        int leftBorder = getLeftBorder(nums, target);
        int rightBorder = getRightBorder(nums, target);

        //根据计算得到的左右边界判断返回值
        // 情况一
        if (leftBorder == -2 || rightBorder == -2) return {-1, -1};
        // 情况三
        if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};
        // 情况二
        return {-1, -1};
    }
};